• 기수법이 무엇인지 알고 이해한다.

• 이진수, 십진수, 16 진수를 서로 변환한다.

• 컴퓨터 메모리의 단위(비트, 바이트, 워드, 더블 워드) 에 대해 안다.

아마 제 강좌를 읽는 분들 중에선 중학교 수학을 접하지 않는 분들도 있을 수 있기 때문에 이 강좌를 작성하게 되었습니다. 3 강에서 이 부분에 대한 내용을 다루고 있으나 질문이 자주 나오는 것 같아서 이렇게 강좌를 올립니다. 사실 이 부분의 내용은 중학교 수학에서는 모두 다루는 내용이므로 꼭 보셔도 되지 않지만 복습 차원에서 한 번쯤 보아도 좋습니다. 또한, 앞으로 중요하게 쓰일 몇 가지 컴퓨터 용어들을 다루고 있으니 (물론 3 강에서도 나옵니다만...) 한 번 보는 것이 좋겠습니다.

여러분은 '수' 와 '숫자' 의 차이를 알고 계십니까? 아마 많은 사람이 모를 텐데 영어로 하면 '수' 는 Number 이고 '숫자' 는 Digit 라 합니다.

'수' 는 어떠한 물질의 양을 나타내는 단위 입니다. '숫자' 는 이를 기록할 수 있도록 시각화 한 것이지요. 예를 들어서, 사과가 100 개 있다는 사실을 보여주기 위해 사과를 100 개 그려야 되면 상당히 곤란하겠지요. 단순히 '100' 이라는 것만 써서 사과가 100 개 있다는 사실을 알 수 있습니다.

그런데 놀라운 점은 우리가 이러한 0,1,2,3,4,5,6,7,8,9 의 숫자들만을 이용하여 수를 표시 할 수 있다는 것이 아닙니다. 우리가 사과 라는 물질을 나타내기 위해 '사과' 라고 쓰지만 사과를 나타내기 위해 꼭 '사과' 라고 써야 하나요? 영어로 'Apple' 이라 쓸 수 도 있고 일본어로 'リンゴ' 라고 쓸 수 있습니다. 수도 마찬가지 입니다. 인간의 손가락이 10개 인지라 수를 10 개의 숫자로 나타내었지만 마음에 안들면 0 과 1 만을 이용할 수 도 있고 100 개의 숫자를 이용할 수 도 있습니다.

이렇게 수를 표현하는 방법을 기수법(Numeral system) 이라 합니다.

수학적 배경 지식 - 밑과 지수

여기서 소개하는 내용은 중학교 1 학년 재학시 배우게 됩니다만, 제 블로그를 방문하는 분들 중에 초등학생들도 적지 않게 있으리라 생각되어 간단히 짚고 넘어가겠습니다.

수학은 '복잡한 것을 단순히!' 라는 목적 하에 발전해 왔습니다. 이것도 이러한 본분을 충실히 따른 것 입니다. 우리는 곱하기 연산을 자주 사용합니다. 그 때 마다 이를 표현하기 위해 곱하기 기호를 사용해야 합니다. 예를 들어 아래 처럼 2 를 100 번 곱한 수를 생각해 봅시다.

$2 \times 2 \times 2 \times \cdots \times 2$

(너무 길어서 약간 생략)

우리는 위 수를 나타내고 싶을 때 마다 위와 같이 2 를 100 번이나 적어야 합니다. 다행이도 수학자들은 위를 단순화 하여 나타내기 위해 아래와 같은 기호를 만들어 냈습니다.

$2^{100} = 2 \times 2 \times 2 \times \cdots \times 2$

정말 훌륭한 생각 아닙니까? 단순히 2 를 100 번 곱했다는 사실을 알려주기 위해서 2 위에 작은 글씨로 100 을 적었습니다. 이 때 아래 '2' 를 '밑(base)' 라 부르고 밑 위에 밑을 몇 번 곱할 지 나타낸 수 100을 '지수(exponent)' 라고 부릅니다. 위 숫자의 경우 밑은 2 가 되고 지수는 100 이 되겠지요.

아마 이해가 잘 안되면 아래와 같은 예를 보시면 됩니다.

$3^5 = 3 \times 3 \times 3 \times 3 \times 3$

$7^2 = 7 \times 7 = 49$

지수에서 가장 중요한 사실은 바로

$(\text{Number})^0 = 1$

라는 사실입니다. Number 에는 어떠한 수도 들어 갈 수 있습니다. (다만 0 제외) 아마 이 부분에서 의아해 하는 사람들이 많을 것 입니다. "어떻게 숫자를 한 번도 안 곱했더니 1 이 될수가 있냐! 수학자 바보들 아니냐!" 말이지요. 하지만 사실 이 값은 사실 수학자들 사에서 약속 처럼 정의한 값이라 생각하면 됩니다. 만일 이 값을 1 이라 하지 않는다면 여러 지수들에 관련된 중요한 법칙들이 성립 되지 않기 때문이죠. 다시말해 어떤 수의 0 승 한 것이 1 이라 생각하는 것은 다른 법칙들이 만족되기 위해 그렇게 약속한 것이다 정도로 알고 계시면 되겠습니다.

십진법, 이진법, 16 진법

현재 아라비아 숫자를 사용하는 우리는 수를 나타내기 위해 10 개의 숫자를 이용하는, 소위 말하는 십진법(decimal) 을 이용하고 있습니다. 정확하게 알려진 것은 아니지만 우리가 '10' 에 그토록 관련이 많은 것이 인간이 10 개의 손가락을 가졌기 때문이라 생각합니다. 아무튼, 우리는 '253' 이란 숫자가 나오면 아래와 같이 생각합니다.

$253 = 2\times 10^2 + 5 \times 10^1 + 3 \times 10^0$

다시 쓰면,

$253 = 200 + 50 + 3$

이 됩니다. 한 가지 주목하실 부분은 바로 한 자리수가 늘어 날 때 마다 그 자리를 나타내는 숫자에 '10' 이 곱해진 다는 것이지요.가장 오른쪽 자리는 1 의 자리, 그 다음 자리는 10 의 자리, 그 다음은 100 의 자리, 그 다음은 1000 의 자리로 말이지요.예를 들어서 253 앞에 7 을 붙인다면

$7253 = 7\times 10^3 + 2\times 10^2 + 5 \times 10^1 + 3 \times 10^0 = 7000 + 200 + 50 + 3$

가 됩니다. 이 것이 바로 십진법의 가장 큰 특징이라고 할 수 있습니다. 자리수가 하나 증가할 때 마다 이 자리를 나타내는 숫자에 10 이 곱해지게 되지요. 또한 중요한 특징으론 십진법이 10 개의 숫자를 사용한다는 것 입니다. 0 부터 9 까지 모두 10 개의 숫자를 이용하지요.

이런 아이디어를 적용 시켜서 이진법을 생각해 봅시다. 컴퓨터는 0 과 1 인 두 종류의 숫자 밖에 표현할 수 없습니다. (전기적 신호가 _on_ 이냐 _off_ 냐에 따라 말이지요) 그러면 컴퓨터는 253 을 어떻게 생각할까요? 컴퓨터는 0 과 1 밖에 생각 못하므로 표현할 수 없다구요? 아닙니다. 컴퓨터도 0 과 1 만을 가지고서 모든 수를 표현 할 수 있습니다. 우리가 10 개의 숫자를 가지고 수를 표현하므로 이를 '십진법' 이라 부르지만 컴퓨터는 두 개의 숫자 만으로 수를 표현하므로 '이진법(Binary)' 라 부릅니다.

예를 들어 6 을 이진수로 나타낸다고 합시다. 그렇다면 우리가 십진법에서 사용한 규칙을 그대로 적용하여 사용하면 아래와 같습니다.

$ 6 = 4 + 2 = 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 = 110_2$

어때요? 규칙이 정확히 동일한가요? 십진법에선 한 자리 늘어날 때 마다 10 이 곱해졌으므로 이진법에선 한 자리 늘어날 때 마다 2 가 곱해집니다. 즉, 가장 오른쪽 자리는 1, 그 다음은 1 에 2 를 곱했으므로 2, 그 다음은 2 에 2를 곱했으므로 4의 자리가 됩니다.

또한 십진법이 0 부터 9 까지의 수를 쓴 만큼 이진법도 0 과 1 만을 사용해야 합니다. 위에 보면 알 수 있듯이 6 을 110 으로 표현하였습니다. 즉, 1 과 0 만을 사용하였습니다.

110 밑에 조그맣게 2 가 표시되어 있는 것이 무엇인지 궁금해 하는 사람들이 있습니다. 이는 '이 수가 이진법으로 표현되어 있습니다' 를 알려주는 기호 입니다. 즉 2 라는 표시가 없다면 이 수가 정말 십진법으로 110을 표현한건지, 아니면 이진법으로 110을 표현한 것인지 알 길이 없기 때문이죠.

이진수가 무엇인지 확실히 감을 잡기 위해 아래의 수들을 보시면 됩니다.

$23 = 16 + 4 + 2 + 1 = 1 \times 2^4 + 0 \times 2^3 + 1 \times 2^2 + 1\times 2^1 + 1 \times 2^0 = 10111_2$

$49 = 32 + 16 + 1 = 1 \times 2^5 + 1 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 + 0\times 2^1 + 1 \times 2^0 = 110001_2$

그렇다면 이제 이진수를 어떻게 십진수로 바꿀 수 있는지 알아 봅시다. 사실, 위의 내용을 잘 이해하였다면 정말 간단합니다.

아래 그림과 같이 하면 됩니다.

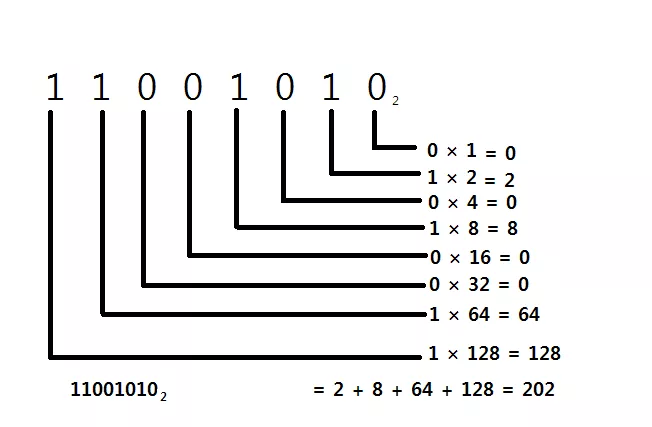
자리수가 하나 올라갈 때 마다 그 자리수의 값이 두 배로 된다는 사실만을 기억하면 됩니다. 하지만 관건은 십진수를 이진수로 어떻게 쉽게 바꾸느냐 입니다. 사실 이는 어렵게 느껴지지만 그 과정은 매우 단순합니다. '2로 나누는 연산' 을 반복해 주면 되지요. 아래 그림을 참조하세요.

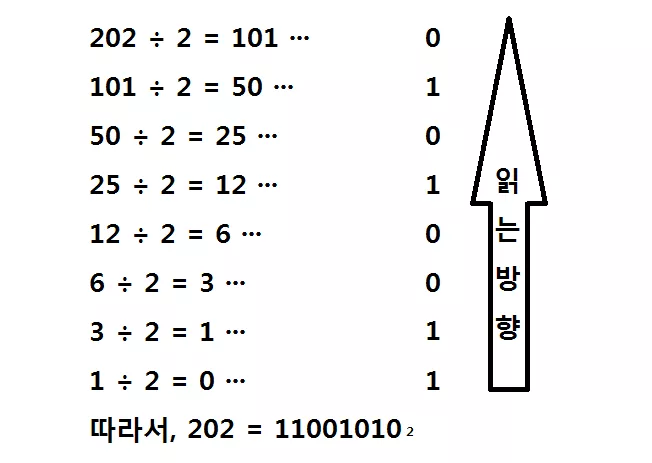
··· 의 기호는 나머지를 뜻합니다. 즉, 25 를 2 로 나누면 몫이 12 고 나머지가 1 이 됩니다. 단순히 십진수를 2 로 계산 나누어서 나온 나머지를 몫이 0 이 될 때 까지 구한 다음에 나머지들만 역순으로 재배치 하면 됩니다. 의외로 단순합니다.

(사실 위 방법이 어떻게 정확한 결과를 도출해 내느냐에 대해 설명해야 하지만 사실 세세히 알 필요도 없고 나중에 다 배우므로 생략하도록 하겠습니다.)

하지만, 이진수는 흔히 수가 너무 커지는 경향이 있습니다. 예를 들어 1024 는 십진수로 4 자리 밖에 안되지만 이진수로는 10000000000 이 되어 무려 11 자리나 됩니다. 1 과 0으로 나타내면 (사람들의 입장에서) 읽기 번거럽기 때문에, 이를 손쉽게 표현하기 위해서 프로그래머들은 보통 16진법을 사용하고 있습니다. 16 진법도 여태까지 사용하였던 아이디어를 동일하게 적용하면 됩니다.

그런데 한가지 주목해야하는 사실은 16 진수가 숫자를 16 개나 필요로 한다는 점입니다. 우리가 사용하는 십진법은 숫자가 10 개만 필요하므로 숫자가 10 종류 밖에 없습니다. 따라서 사람들은 16 진수를 위해 필요한 숫자 6개를 알파벳을 이용하여 숫자를 표현하였습니다. 즉 10 에 대응되는 것이 A, 11 에는 B, 12 에는 C, 13 에는 D, 14 에는 E, 15 에는 F 입니다. 16 진수는 0,1,2,...,9,A,B,C,D,E,F 를 이용하여 숫자를 표현 합니다.

$123 = 7 \times 16 + 11 = \text{0x7B}$

16 진수도 마찬가지로 같은 논리를 적용합니다. 한 자리가 늘어날 때 마다 16 을 곱하면 되는 것이지요. 이 때, 7B 앞에 붙은 0x 는 이 수가 16 진수로 나타나있다는 것을 알려줍니다. 좀 더 이해를 돕기 위해 몇 가지 예를 들겠습니다.

$19 = 16 + 3 = \text{0x13}$

$16782 = 4 \times 16^3 + 1 \times 16^2 + 8 \times 16^1 + 14 \times 16^0 = \text{0x418E}$

16 진수를 십진수로 바꾸거나 십진수를 16 진수로 바꾸는 일은 앞서 이진수의 경우와 동일합니다. (다만, 2 대신 16 으로 곱하거나 나누어 주어야 한다는 점 말고는) 이는 단순하지만 계산이 지저분 하고 복잡하였죠. 하지만 16 진수를 이진수로, 이진수를 16 진수로 바꾸는 방법은 매우 간단합니다.

먼저 16 진수를 이진수로 바꾸는 방법을 살펴 봅시다. 이는 단순히 16 진수의 각 자리수를 4 자리 (반드시) 이진수로 변환해 주면 됩니다.

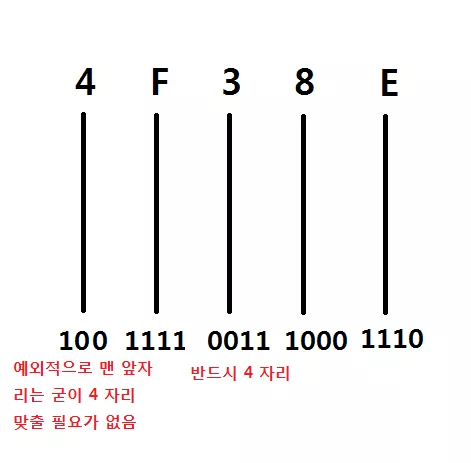
위와 같이 0x4F38E 를 2 진수로 변환하면 1001111001110001110 가 됩니다.

마찬가지로 이진수를 16 진수로 바꾸어 주는 것도 간단합니다. 단지 4 자리씩 뒤에서 부터 끊어서 읽으면 되지요. 아래 그림을 보면 알 수 있습니다.

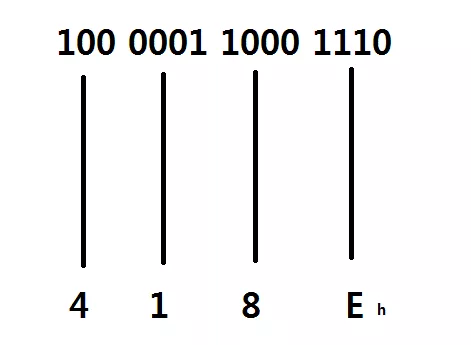
컴퓨터 메모리의 단위

컴퓨터에 대해 조금이나마 공부한 사람이라면 컴퓨터에 데이터를 저장하는 공간은 크게 두 부류로 나눌 수 있다고 들었을 것입니다. 컴퓨터를 종료하면 데이터가 날아가는 휘발성 메모리와 컴퓨터를 종료해도 데이터가 날아가지 않는 비휘발성 메모리로 말이지요.

이 때, 휘발성 메모리의 대표적인 주자로 램(RAM, Random Access Memory) 과 비휘발성 메모리의 대표 주자로 롬(ROM, Read Only Memory 흔히 말하는 CD - ROM 이나 DVD - ROM, 아니면 우리 메인보드 Bios 에 박혀있는 롬 등등) 나 하드 디스크 등이 있겠지요.

이 때, 앞으로 저의 강좌에서 주로 '메모리' 라 말하는 것은 휘발성 메모리인 RAM 을 말합니다. RAM 은 하드 디스크나 CD 와는 달리 속도가 매우 빠릅니다. (CD 휭 돌아가는 소리 들어 보셨죠?) 왜냐하면 RAM 의 경우 데이터의 랜덤하게 접근할 수 있는데 하드 디스크나 CD 는 순차적으로 접근 해야 되기 때문이죠.

쉽게 말해 우리가 아파트 713 호에 사는 철수를 찾는다고 합시다. 철수가 만일 RAM 아파트에 산다면 단박에 713 호에 산다는 것을 알 수 있지만 하드 디스크 아파트에 산다면 101 호 부터 모든 주민들 일일히 찾아 713 호 까지 찾아 보아야 한다는 뜻 입니다.

이런 매우 빠른 메모리의 특성 때문에 컴퓨터는 대부분의 데이터들은 메모리에 보관해 놓고 작업을 하게 됩니다. 물론 메모리는 전원이 꺼지면 모두 날아가기 때문에 중요한 데이터들은 틈틈히 하드 디스크에 저장하게 되지요.

컴퓨터의 한 개의 메모리 소자는 0 혹은 1 의 값을 보관할 수 있습니다. 이 이진수 한 자리를 가리켜 비트(Bit) 라고 합니다. 따라서, 1 개의 비트는 0 또는 1 의 값을 보관할 수 있겠지요. 하지만 이는 너무나 작은 양입니다. 보통 우리는 1 보다 훨씬 큰 수들을 다루기 때문이지요. 그래서, 사람들은 이렇게 8 개의 비트를 묶어서 바이트(Byte) 라고 부릅니다. 즉, 8 비트는 1 바이트 이지요.

(참고로 4 비트를 특별히 묶어서 니블(nibble) 이라 부릅니다만, 잘 쓰이지는 않습니다)

8 비트로 나타낼 수 있는 수, 다시말해 8 자리 이진수로 나타낼 수 있는 최대의 수는 아래와 같이

$00000000_2 \sim 11111111_2 = 0 \sim 255 = 0 \sim \text{0xFF}$

0 부터 255 로 총 256 개의 수를 나타내게 됩니다.

그 다음 단위로 워드(Word) 라고 부르는 단위가 있습니다. 컴퓨터에서 연산을 담당하는 CPU 에는 레지스터(register) 라는 작은 메모리 공간이 있는데, 이곳에다가 값을 불러다 놓고 연산을 수행하게 됩니다.

예를 들어서 a + b 를 하기 위해서는 a 와 b 의 값을 어디다 적어놓아야지, a + b 를 할 수 있는 것처럼, CPU 에서 연산을 수행하기 위해 잠시 써놓는 부분을 레지스터라고 합니다.

이러한 레지스터의 크기는 컴퓨터 상에서 연산이 실행되는 최소 단위라고 볼 수 있고, 이 크기를 워드 라고 부릅니다. 32 비트 컴퓨터 시절에서는 이 1 워드가 32 비트, 즉 4 바이트 였지만, 지금 대다수의 여러분이 사용하는 64 비트 컴퓨터의 경우 1 워드가 64 비트, 즉 8 바이트가 됩니다.

이것으로 여러분이 기수법과 컴퓨터 메모리의 단위에 대해 알아보았습니다. 그럼, 이번 강의는 여기서 마치도록 하죠.

댓글이 229 개 있습니다!

강좌에 관련 없이 궁금한 내용은 여기를 사용해주세요

다음으로 로그인

또는 직접 입력하세요 (댓글 수정시 비밀번호가 필요합니다)

댓글 달기

댓글을 불러오는 중입니다..