이전 글에서 자료 구조란 데이터를 효율적으로 저장하고, 또 효율적으로 불러 올 수 있게 해주는 도구라고 하였습니다. 이 얼마나 효율적으로 불러오는지 객관적으로 표현하기 위해선, 보통 자료 구조가 보관하고 있는 데이터의 개수를 기준으로 (보통 $N$ 으로 씁니다.) 알고리즘 강의에서도 다루었던 Big-O 표현법 을 사용해서 나타냅니다.

그렇다면 이번 글에서는 맛보기로 컴퓨터 상에서 존재하는 가장 간단한 자료 구조인 배열에 대해서 이야기 해보고자 합니다.

컴퓨터에 데이터가 보관되는 곳

컴퓨터의 저장 장치는 크게 컴퓨터 전원을 끄면 날아가는 휘발성 메모리 (Volatile memory)와, 컴퓨터의 전원을 꺼도 유지되는 비휘발성 메모리로 구분됩니다. 이 때 여러분이 사용하는 데스크탑 컴퓨터라면, 보통 휘발성 메모리는 램(RAM) 이라는 저장장치가 담당하고, 비휘발성 메모리는 하드 디스크나 SSD 가 담당하게 됩니다.

램의 속도는 하드 디스크나 SSD 에 비해서 몇 만배 이상 빠르기 때문에 CPU 에서 데이터를 처리할 때에는 먼저 하드에서 필요한 데이터를 불러온 뒤에, 램과 CPU 가 소통하면서 작업을 수행하죠. 따라서 램이 데이터를 어떠한 방식으로 보관하는지 아는 것이 중요합니다.

램은 마치 수 많은 방들로 이루어진 호텔이라고 생각하면 됩니다. 각 방에는 데이터를 보관할 수 있는데, 현대의 램의 경우 각 방에 1 바이트 (이진수로 8 자리 수) 만큼의 데이터를 보관할 수 있습니다.

호텔의 경우 각 방에 번호가 있죠. 램도 마찬가지 입니다. 각각의 1 바이트 짜리 방 마다 고유의 주소가 부여되어 있는데 이 값을 주소값 이라고 부릅니다. 만일 CPU 에서 데이터를 필요로 한다면 주소 1234 에 위치해 있는 데이터 가져와 이런 식으로 이야기 합니다.

여기서 램의 가장 중요한 특징이 하나 있습니다. 바로 램의 어느 위치에 있는 데이터라도 일정한 속도로 읽고 쓸 수 수 있다는 점입니다. 즉 주소값 1 에 위치한 데이터를 읽든, 주소값 10000000 에 위치한 데이터를 읽든 해당 데이터를 읽는 속도는 동일합니다. 마찬가지로 주소값 1 에 위치에 데이터를 쓰든, 주소값 10000000 의 위치에 데이터를 쓰든, 걸리는 시간은 동일합니다.

이렇게 위치에 따라 데이터를 읽고 쓰는데 걸리는 시간이 똑같다는 점에서 이 임의 접근 메모리 - Random Access Memory, 즉 RAM 이라고 부르는 것입니다.

참고로 하드 디스크의 경우 위치에 따라 읽는데 걸리는 시간이 다릅니다.

하드 디스크의 경우 위 사진에 보이는 원반이 데이터를 저장하는 곳인데, 해당 원반이 빙글빙글 돌아가면서 끝에 보이는 뾰족한 탐침이 데이터를 읽어들입니다. 따라서 하드 디스크의 경우 순차적으로 읽는 것 은 비교적 빠르지만 (디스크를 쭈르륵 한 방향으로 돌리면서 읽으면 되니까요) 임의의 위치에 펴져 있는 데이터를 읽는 것은 매우 느립니다.

램을 바탕으로 한 가장 간단한 자료구조 - 배열

그렇다면 여러분에게 이러한 램을 딱 던져주면서 이걸 바탕으로 자료 구조를 만들어봐 라고 이야기 한다면 어떤 식으로 구성을 할 것인가요? 간단합니다. 램의 방들을 그냥 데이터를 보관하는 용도로 사용하면 되는 것입니다. 이 때 임의의 위치의 방들을 사용하게 되면 해당 방들의 위치를 따로 보관해야 하기 때문에 그냥 어느 특정 지점 부터 연속적인 방들을 데이터 보관 용도로 사용하면 됩니다.

이러한 형태의 자료 구조를 바로 배열 (Array) 라고 합니다. C 나 C++ 을 배우신 분들은 아마 지겹게 들어봤을 이름이기도 하죠.

이 배열을 사용하는 방법은 간단합니다. 데이터를 저장하기 위해서는 몇 번째 칸에 데이터를 넣을 지 명시해주면 됩니다. 예를 들어서 3 번째 칸에 데이터를 넣고 싶다면, 배열의 시작 위치로 부터 3 만큼 떨어진 곳에 그냥 데이터를 쓰면 되겠죠.

보통 배열을 표기할 때 arr[3] 과 같은 식으로 표기합니다. arr 은 배열의 이름이고, 뒤에 [3] 해당 배열 안에 몇 번째 원소를 의미하는지 지칭합니다. 통상적으로 배열의 원소 번호는 0 부터 시작하므로, arr[3] 은 4 번째 원소를 의미 합니다.

그렇다면 이 배열에서 원소를 접근하는데 얼마나 걸리는지 생각해봅시다. 예를 들어서 arr[n] 을 읽기 위해서는 배열의 시작 주소에서 $n$ 만큼 더한 곳에 있는 데이터를 읽으면 됩니다. 이 때 메모리에서 임의의 주소값에 위치한 데이터는 일정 시간으로 접근할 수 있다고 하였습니다.

따라서 arr[n] 을 하는데 필요한 작업은

1. 배열의 시작 주소에서 n 을 더하기

2. 메모리에 해당 주소를 요청하기

인데 위 1, 2 작업 모두 배열 전체의 크기에 관련되지 않습니다. 따라서 Big-O 표기법으로 배열에서의 원소 접근은 $\mathcal{O}(1)$ 이라고 보시면 됩니다.

$\mathcal{O}(1)$ 은 자료 구조가 제공할 수 있는 시간 복잡도 중에서 가장 좋은 것입니다. 배열의 크기가 아무리 크더라도 $\mathcal{O}(1)$ 만에 모든 원소들에 접근을 할 수 있다니요! 배열은 그야말로 완벽한 자료 구조임에 틀림 없습니다.

하지만 이렇게 이야기가 끝났다면 그 뒤로 무수히 많은 자료 구조들이 쏟아져 나오지 않았겠죠. 배열을 한 가지 치명적인 단점이 있습니다. 바로 배열의 크기를 한 번 정한다면 바꿀 수 없다 라는 문제가 있습니다.

배열의 문제

일단 배열을 메모리 상에 정의를 하면 해당 배열을 더이상 늘릴 수 없습니다. 왜냐하면 배열 뒤에 다른 무언가가 해당 공간을 사용하고 있을 수 있기 때문이죠.

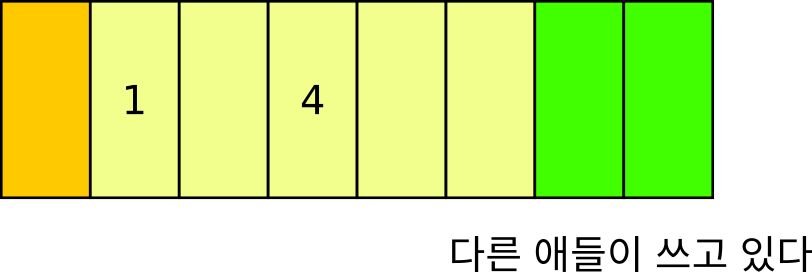
위 처럼 우리의 배열 (노란색 영역) 바로 뒤에 다른 데이터 (초록색 영역) 들이 와 있는 것을 볼 수 있습니다. 배열은 메모리 상에서 반드시 연속적으로 존재해야 하기 때문에 (그래야 시작 주소에서 n 을 더한 위치에 우리의 데이터가 딱 있겠죠) 다른 빈 공간에 늘어난 공간을 줄 수 있는 노릇이 아닙니다.

뿐만 아니라 배열을 다른 넓은 공간으로 쉽게 움직일 수 도 없는 노릇입니다. 왜냐하면 다른 곳으로 이사가기 위해선 해당 배열 안의 모든 데이터들을 복사해야 하기 때문이죠.

따라서 우리가 배열에 나는 딱 3 개만 저장할꺼야 라고 미리 알고 있지 않는 이상 배열의 크기를 크게 잡아야 하는데 이는 공간의 낭비로 이어지겠죠. 배열을 원소 1000 개 만 담게 만들었는데 막상 1 개만 사용하면 나머지 공간이 얼마나 아깝겠습니까.

더 큰 문제는 배열의 크기가 모자라서 더이상 새로운 원소를 추가하지 못할 때 입니다. 이 경우 해당 데이터를 포기하던지, 기존의 원소에 덮어 씌어야 하겠죠.

따라서 이 배열이라는 아주 기본적인 구조를 바탕으로 그 뒤로 여러가지 자료 구조들이 파생되어서 나오게 되었습니다.

배열 실제로 사용하기

거의 모든 컴퓨터 언어는 배열을 거의 기본적인 타입으로 사용할 수 있게 지원하고 있습니다. 예를 들어서 C++ 의 경우

#include <iostream>
#include <array>

int main() {
  // 크기가 5 인 배열
  int arr[5] = {1, 2, 3, 4, 5};

  // 크기가 3 인 배열
  std::array<int, 3> arr2 = {1, 2, 3};

  for (int i = 0; i < 5; i++) {
    std::cout << arr[i] << std::endl;
  }

  for (int i = 0; i < arr2.size(); i++) {
    std::cout << arr2[i] << std::endl;
  }
}

위 처럼 두 가지 형태로 배열을 정의할 수 있는데,

// 크기가 5 인 배열
int arr[5] = {1, 2, 3, 4, 5};

이 방식은 C 언어 상에서 크기가 5 이고 각 원소가 int 인 배열을 정의하는 방식이고,

// 크기가 3 인 배열
std::array<int, 3> arr2 = {1, 2, 3};

위 방식은 C++ 에서 추가된 std::array 를 사용해서 크기가 3 이고 각 원소가 int 인 배열을 정의하는 방식입니다. C++ 에서 배열을 사용할 때에는 되도록이면 std::array 를 사용하는 것을 추천드립니다.

배열의 원소에 접근하는 방법은 위에서 이야기 한 것 처럼 arr[1] 과 같은 식으로 [] 안에 선택하고자 하는 원소의 위치를 전달하면 됩니다.

마찬가지로 파이썬의 경우:

a = [1,2,3]
print(a[1])

위 처럼 a 라는 배열을 정의할 수 있습니다. 사실 파이썬에서는 엄밀한 임의의 배열은 없는데 (왜냐하면 위 a 는 사실 그 크기를 늘리거나 줄일 수 있습니다) 그래도 거의 배열과 같이 동작한다고 보시면 됩니다.

아무튼 배열의 특성을 정리해보자면 다음과 같습니다.

작업	시간 복잡도
임의의 원소 읽기	$\mathcal{O}(1)$
임의의 원소 쓰기	$\mathcal{O}(1)$
크기 늘리기	불가능
사용 공간	$\mathcal{O}(n)$

이번 글에서 모든 자료 구조들의 근간을 이루는 가장 기초적인 자료 구조인 배열에 대해서 다루어보았습니다. 다음 글에서는 배열의 단점을 보완한 크기를 바꿀 수 있는 배열 에 대해서 다루어보고자 합니다.