모두의 코드
모두의 알고리즘 - 1. 어떤 알고리즘이 효율적인가?
안녕하세요 여러분! 이번 강좌에서는 먼저 여러가지 알고리즘에 대해 다루기 앞서, 어떤 알고리즘이 효율 적이라 할 때 이를 나타내는 지표들에 대해 다루어 보도록 하겠습니다.
효율적인 알고리즘이란?
앞서 알고리즘이란 어떤 문제를 해결하는 방식이라고 하였습니다. 하지만 여기서 중요한 점은 어떤 문제를 어떻게 하면 잘 해결하느냐 입니다. 즉 동일한 문제를 해결하는 알고리즘이라 하더라도, 좀 안좋은 알고리즘은 오래 걸리겠지만, 효율적인 알고리즘이라면 훨씬 빠른 속도로 문제를 풀 수 있을 것입니다.
그렇다면, 여기서 중요한 것이 이 빠른 속도라는 것을 어떻게 하면 체계적으로 표현할 수 있느냐 입니다. 만약에 이 속도를 해당 알고리즘으로 문제를 해결하는데 걸리는 시간이라고 정의를 해봅시다. 문제는 이런식으로 정의를 하게 된다면, 컴퓨터 마다 그 결과가 제각각이 된다는 문제가 생깁니다.
따라서 컴퓨터 과학자들이 택한 방식은 그 알고리즘으로 문제를 해결하는 동안 총 몇 번의 연산을 수행하느냐가 되었습니다.
예를 들어서 1 부터 100 까지 더하는 연산을 수행한다고 해봅시다. 만약에 단순하게 1 부터 100 까지 쭈르륵 더한다면, 총 100 번의 연산을 수행하겠지요.
하지만, 좀 더 머리를 써서 등차수열의 합이 $\frac{n(n+1)}{2}$ 이 된다는 공식을 사용한다면, 덧셈 한번, 곱셈 한번, 나눗셈 한번 총 3번의 연산으로 답을 구할 수 있습니다.
그렇다면, 좀 더 확장해서 1 부터 n 까지를 더한 값을 구한다고 생각해봅시다. 단순한 알고리즘으로는 총 $n$ 번의 연산을 수행하겠지만, 좀 더 똑똑하게 공식을 사용하는 알고리즘의 경우 여전히 3 번의 연산으로 끝낼 수 있습니다. 즉, 두 번째 방식이 분명 첫 번째 방식 보다는 훨씬 빠르게 수행될 것입니다.
이렇게, 알고리즘의 속도는 어떠한 크기의 입력값($n$)에 대해서 이 알고리즘을 수행하는 동안 몇 번의 연산을 실행하는지로 나타내며, 이를 시간 복잡도(time complexity) 라고 부릅니다.
우리의 단순 덧셈 알고리즘의 경우 입력값(여기서는 $n$)이 커지면 커질 수 록 알고리즘의 시간 복잡도도 더 커집니다 (정확히 말하자면 $n$ 에 비례해서 커지겠지요). 반면에 두 번째 공식을 사용한 알고리즘의 경우 입력값의 크기와는 무관하게, 항상 거의 상수 시간 안에 처리됩니다.
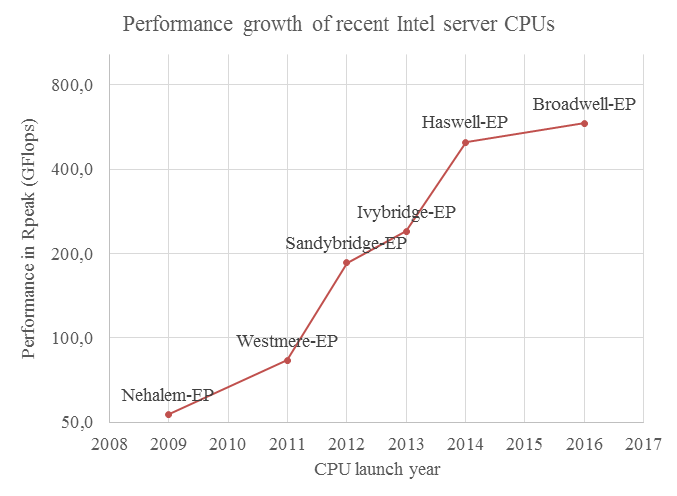
시간 복잡도가 매우 중요한 이유는 실제 이 알고리즘의 수행 시간이 얼마나 걸리는지 알려주는 척도와 거의 직결되기 때문입니다. 당연하게도 알고리즘이 요구하는 연산의 속도가 적으면 적을 수 록 실제 컴퓨터에서도 대부분 더 빠르게 처리됩니다.
물론 옛날 처럼 대략 2년 마다 CPU 집적도가 두 배씩 증가하는 무어의 법칙(Moore's Law) 가 딱딱 들어맞던 때에는 더 빨리 돌아가는 알고리즘을 고민할 시간에 차라리 새 CPU 를 사는 것이 더 나앗을지도 모릅니다. 예컨대 지금 여러분이 사용하는 CPU 는 1993년에 세상에서 제일 빨랐던 슈퍼 컴퓨터 보다도 아마 빠를 것입니다.
하지만 이제는 더이상 예전처럼 컴퓨터 하드웨어의 발전 속도가 빠르지 않기 때문에, 더 빠른 알고리즘을 고민하는 것이 매우 중요합니다.
두 번째로 알고리즘의 효율성을 평가하는데 있어서 중요한 점으로 얼마만큼의 메모리를 사용하느냐가 있습니다.
1 부터 $n$ 까지의 덧셈을 수행하는 알고리즘을 조금 특이한 방법으로 만들어볼 것입니다. 일단, $n$ 의 범위는 int 의 범위라고 가정을 한다면 $n$ 은 최대 $2^{32}$ 이 되겠지요. 그런 다음에, 큰 배열을 생성한 다음, 첫 번째 원소에는 그냥 1, 두 번째 원소에는 1 부터 2 까지 더한거, 세 번째 원소에는 1 부터 3 까지 더한거, ... 쭉 해서 $n$ 번째 원소에는 1 부터 $n$ 까지 더한거를 저장해놓습니다.
그런 다음에, 사용자가 임의의 $n$ 에 대해서 1 부터 $n$ 까지 더한 값을 요청한다면, 덧셈을 새로 수행할 필요 없이 그냥 배열의 $n$ 번째 원소를 리턴해주면 됩니다. 만약에, 앞서 배열을 생성하는 작업을 무시한다면 (아니면 남이 만들어놓은 배열을 그냥 가져다 쓴다고 생각하셔도 됩니다), 사용자에 요청에 대해서 단 한 번의 연산 (배열의 $n$ 번째 원소를 가져옴)으로 덧셈을 수행할 수 있습니다.
즉, 이 알고리즘의 시간 복잡도는 단 1 이 되겠지요. 그렇다면 이 알고리즘은 효율적인 것일까요? 아마 아무도 그렇게 생각하지 않을 것입니다. 왜냐하면 크기가 무려 $2^{32}$, 즉 4 기가 바이트에 달하는 배열이 필요하기 때문이지요.
이러한 문제 때문에 시간 복잡도와는 별개로, 알고리즘이 작동하는데 메모리를 얼마나 사용하는지 나타내는 메모리 복잡도(Memory complexity) (혹은 공간 복잡도(Space complexity) 라고도 합니다) 도 알고리즘의 중요한 특징이 됩니다. 이 바보 같은 알고리즘의 경우 메모리 복잡도가 int 의 최대 크기 만큼 되겠네요.
반면에 우리가 처음에 다루었던 두 개의 알고리즘의 경우 한 몇 바이트 정도면 충분할 것입니다. 이 메모리 복잡도가 중요한 이유 역시, 실제 컴퓨터의 경우 메모리의 크기가 한정되어 있기 때문입니다. 따라서, 알고리즘을 설계할 때 이 알고리즘의 얼마나 많은 메모리를 소모하는지 확인하는 것도 중요합니다.
정리하자면, 좋은 알고리즘이란
시간 복잡도가 비교적 낮고
메모리 복잡도 역시 비교적 낮은
알고리즘을 의미합니다. 보통 둘 다 낮추는 것은 힘들어서, 시간이나 메모리 복잡도 둘 중 하나를 많이 낮추는 쪽으로 가는데, 메모리는 돈으로 살 수 있지만, 시간을 돈 주고 살 수 있는 것이 아니기 때문에 대개 시간 복잡도를 낮추는 것을 중점으로 합니다.
Best, Worst, Average running time
앞서 컴퓨터에서 알고리즘의 시간 복잡도를 이야기 할 때, 입력값의 크기가 $n$ 일 때 몇 번의 연산을 수행하는지로 나타낸다고 하였습니다.
그런데 문제는 위에 나왔던 1 부터 $n$ 까지 더하는 알고리즘과 같은 간단한 경우 말고는, 알고리즘의 연산 횟수가 단순히 $n$ 에 의해 결정되는 경우는 많지 않습니다.
예를 들어서 우리가 문자열을 순서대로 정렬하는 알고리즘을 만들었다고 생각해봅시다. 같은 $n$ 개의 문자열이 있더라도, 만약에 문자열이 이미 정렬된 상태라면, $0$ 번의 연산으로도 데이터를 정렬 시킬 수 있을 것입니다 (이미 정렬되어있으니까요). 하지만, 데이터가 무작위로 있는 경우 여러번의 연산을 수행해야겠지요.
따라서, 이 알고리즘의 입력값이 $n$ 일 때 정확히 몇 번 연산을 하느냐에 대한 질문에는 딱히 대답할 수 없습니다. 그 대신에
이 알고리즘의 입력값이 $n$ 일 때 최대 몇 번의 연산을 하느냐?
와
이 알고리즘의 입력값이 $n$ 일 때 최소 몇 번의 연산을 하느냐?
가 더 의미 있는 질문이겠지요. 이를 보통 Best case running time 과 Worst case running time 이라고 일컫습니다.
물론 이 두 질문은 매우 극단적이기 때문에, 만약에 이 알고리즘이 보통 어떻게 작동하는지가 궁금하다면
이 알고리즘의 입력값이 $n$ 일 때 평균적으로 몇 번의 연산을 하느냐?
로 알고리즘의 시간 복잡도를 표현하게 됩니다. 이를 보통 Average case running time 이라고 합니다.
알고리즘의 시간 복잡도가 최대와 최소의 간격이 적으면 적을 수 록 좋습니다. 왜냐하면 안정적으로 동일한 성능을 보장한다는 뜻이니까요. 대개 자주 쓰이는 알고리즘들은 최대와 최소 횟수가 비슷한 경우가 많습니다.
점근적 표기법 (Asymptotic notation)
예를 들어서, 평균 연산 횟수가 $n^2 + 100n + 2$ 인 알고리즘을 생각해봅시다. 만약에 이 알고리즘의 시간 복잡도를 그냥 $n^2$ 이라고 그러면 어떨까요? 물론 $n$ 이 작을 때에는 오차가 클 것입니다.
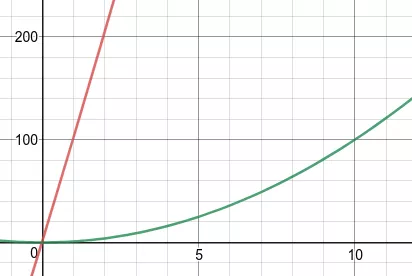
위 그림의 경우 빨간색이 $n^2 + 100n + 2$ 그래프 이고, 초록색이 $n^2$ 을 나타낸 그래프 입니다. 위와 같이 $n$ 이 작을 경우 $n^2 + 100n + 2$ 가 $n^2$ 보다 훨씬 큰 것을 알 수 있습니다.
하지만 $n$ 이 커진다면 어떨까요?
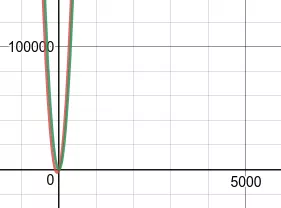
위 그림에서도 보여지듯이, 두 그래프의 차이가 거의 없다는 것이 보입니다. 그도 그럴 것이, 두 그래프의 차이는 $100n + 2$ 인데, $n$ 이 5000 정도 된다면, $100n + 2$ 가 원래의 그래프에서 담당하는 양이
$\frac{100 \cdot 5000 + 2}{5000^2 + 100 \cdot 5000 + 2} \approx 2\%$
2 퍼센트 밖에 되지 않기 때문입니다. 물론 이 값은 $n$ 이 점점 커지면 커질 수 록 작아질 것입니다. 따라서, 굳이 이 알고리즘의 시간 복잡도를 표현하는데 구질구질 하게 끝에 $100n + 2$ 를 붙일 필요가 사라졌습니다. 왜냐하면 어차피 $n$ 이 커지면 그 효과는 미미 하기 때문이지요.
컴퓨터로 알고리즘을 돌릴 때 $n$ 은 대개 매우 크기 마련입니다. 물론 $n$ 이 작다면, $100n + 2$ 의 영향은 오히려 $n^2$ 보다 크겠지만, 일반적인 상황에선 굳이 그 항을 포함시키지 않아도 알고리즘의 실행 성능을 가늠하는데에는 큰 영향이 없습니다.
따라서, 컴퓨터 과학에서는 흔히 알고리즘의 시간 복잡도를 이야기 할 때 점근적 표기법 (Asymptotic notation)을 사용합니다. 점근적 표기법이란, 어떤 함수가 $n$ 이 클 때, 다른 어떤 함수로 근사될 수 있는지를 이야기 합니다.
위 경우 $n^2 + 100n + 2$ 의 경우 $n$ 이 커질 때 $n^2$ 으로 근사할 수 있고, 이를
$ n^2 + 100n + 2 = \mathcal{O}(n^2)$
로 표현합니다. 이를 보통 Big-$\mathcal{O}$ 표기법이라 부릅니다.
수학적으로 엄밀히 정의하자면 다음과 같습니다.
함수 $f(x), g(x)$ 에 대해 $f(x)$ 가 $\mathcal{O}(g(x))$ 를 만족한다면, $x > x_0$ 를 만족하는 모든 $x$ 에 대해 $|f(x)| \le M|g(x)|$ 인 양의 실수 $M$ 과 $x_0$ 가 존재한다.
즉 $O$ 안에 들어가는 함수는 근사하려는 함수의 상한선 을 담당하게 됩니다. 물론, 하한선을 의미하는 Big-$\Omega$ 표기법도 있고, 상한 하한을 모두 포함하는 Big-$\Theta$ 표기법도 있습니다. 당연히도 $\Theta$ 표기법이 좀 더 엄밀한 범위를 나타내기는 하지만 대부분의 경우 Big-O 표기법으로 알고리즘의 복잡도를 나타냅니다.
그림으로 보면 아래와 같습니다.
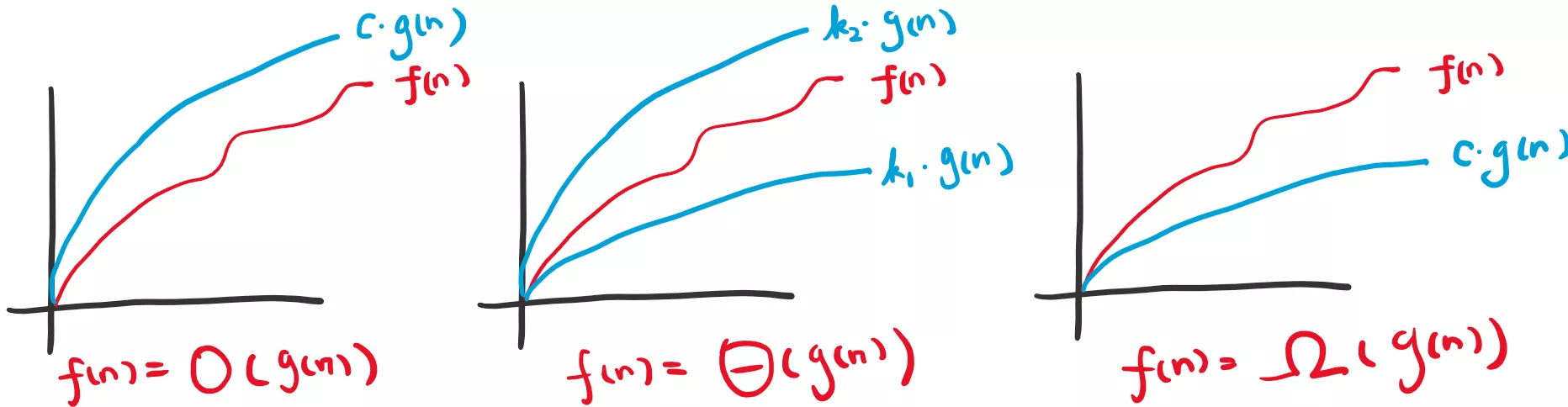
Big-$O$ 의 정의가 조금 어렵긴 하지만, 그냥 쉽게 생각하면, 그 함수의 최고차항이 대부분 Big-O 가 됩니다. 예를 들어보자면
$f(n) = 10n^3 + 2000n^2 + 100000n\rightarrow f(n) = \mathcal{O}(n^3)$. 왜냐하면 최고차항이 $n^3$ 이니까. 물론 최고 차항의 계수도 무시해도 됩니다. (왜 그런지는 위 Big-O 의 정의를 다시 한번 읽어보세요)
$f(n) = e^n + n^{10000}\rightarrow f(n) = \mathcal{O}(e^n)$. 지수 함수는 그 어떠한 다항 함수보다도 빠르게 증가한다고 생각하면 됩니다. 만약에, 알고리즘이 지수 함수적으로 늘어난다면, $n$ 이 조금만 커져도 컴퓨터가 계산할 수 없을 만큼 연산의 양이 많아집니다.
$f(n) = 100n\log n + n\rightarrow f(n) = \mathcal{O}(n\log n)$. 많은 경우 알고리즘에 $\log$ 가 들어가게 됩니다. 보통은 밑이 2 인 $\log$ 를 사용하지만, 크게 중요하지는 않습니다. (왜 그럴까요?)
$f(n) = 100n\log n + n^{1.001}\rightarrow f(n) = \mathcal{O}(n^{1.001})$. 지수 함수와는 반대로 로그 함수는 어떠한 다항 함수 보다도 느리게 증가합니다. 즉 $\log_n$ 보다 $n^{0.001}$ 이 훨씬 빠르게 증가합니다.
$f(n) = 100\rightarrow f(n) = \mathcal{O}(1)$. 보통 상수 함수는 $\mathcal{O}(1)$ 로 나타냅니다.
Big-O 의 종류 별로 얼마나 빠르게 증가하는지 보고 싶다면 아래의 그림을 보면 됩니다.
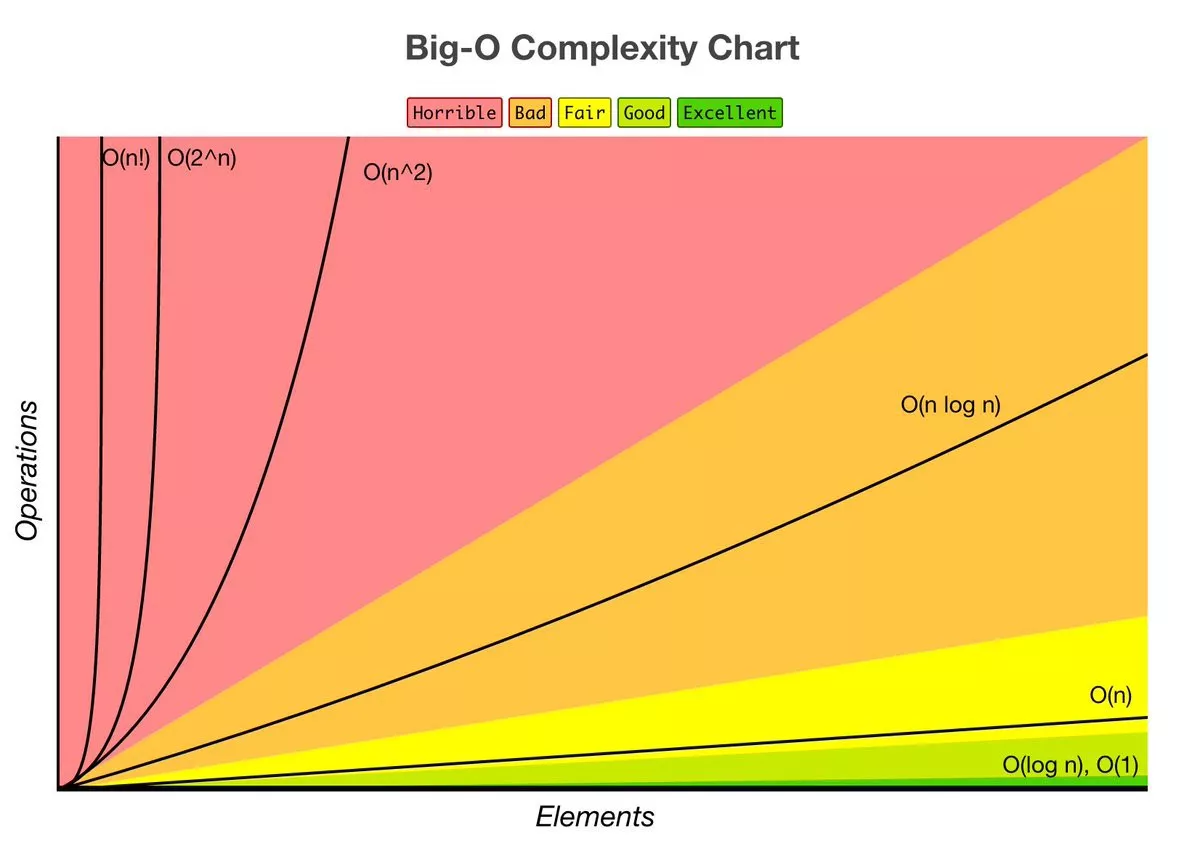
보시다시피, 만약에 내가 만든 알고리즘이 $O(n!)$ 이나 $O(2^n)$ 단위라면, 알고리즘의 개선을 심각하게 고민해봐야 합니다. 보통 $n$ 이 100 만 넘어가도 연산 불가능한 양이 됩니다.
대부분의 경우에는 알고리즘의 복잡도를 $O(n^2)$ 안으로 끊을 수 있을 것입니다. 보통 $n^2$ 알고리즘에서 머리를 조금 쓰면 $O(n\log n)$ 으로 만들 수 있는 경우가 많습니다. $\log n$ 은 매우 느리게 증가하므로, 적당한 범위 안에 $n$ 이라면 거의 $O(n)$ 과 비슷한 속도로 동작합니다.
가장 이상적인 상황은 $O(\log n)$ 이거나 $O(1)$ 인데, 이 말은 데이터 전부를 보지 않고도 알고리즘을 실행할 수 있다 와 동일합니다. 보통, 이와 같은 알고리즘이 돌아가는 경우 여러 특수한 상황에 정의되어 있어야만 합니다.
이 것으로 이번 강좌를 마치도록 하겠습니다. 다음 강좌에서 부터는 본격적으로 알고리즘에 대해 다루어 볼 것입니다.
생각 해보기
문제 1
버블 소트(Bubble sort) 의 최악의 경우, 최고의 경우, 평균적인 경우의 시간 복잡도는 어떻게 될까요?
댓글을 불러오는 중입니다..