모두의 코드
모두의 알고리즘 - 2 - 4. k 번째 원소를 찾는 알고리즘 - QuickSelect
안녕하세요 여러분. 이번 강좌에서는 지난 퀵 정렬 강좌에서 배운 분할 정복 기법을 활용해서 정렬했을 때 $k$ 번째 원소를 빠르게 찾는 알고리즘인 QuickSelect 와 이를 보완하는 알고리즘인 Medians of medians 라는 알고리즘을 소개하려고 합니다.
왜 어려운가?
일반적인 $k$ 에 대해 어떻게 찾을지에 대해 생각하기 전에 먼저 몇몇 케이스들을 살펴보도록 하겠습니다. 전체 원소의 개수가 $N$ 이라고 생각할 때, $k$ 가 1 이나 $N$ 이면 어떨까요? 이 말은 즉슨, 원소들의 최대값과 최소값을 찾는 알고리즘을 말합니다.
이 경우, 최대값과 최소값을 $\mathcal{O}(N)$ 으로 찾을 수 있습니다. 왜냐하면 예컨대 최대값을 찾는다면, 첫 번째 원소를 최대값이라 가정한 뒤에, 전체 원소들의 나열을 쭈르륵 스캔해가면서 현재 최대값 보다 큰 원소가 나타난다면 최대값을 해당 원소로 업데이트 하면 되기 때문이지요.
그렇다면 $k$ 가 2 나 $N - 1$ 일 경우는요? 두 번째로 크거나 작은 원소는 어떻게 찾을 까요? 이번에는 그냥 후보군을 2 개로 잡으면 됩니다. 맨 앞에서 부터 원소들을 쭈르륵 스캔하면서 현재 가장 크거나 작은 원소 두 개를 기록해나가면 되는 것이지요. 따라서 공간 복잡도 $\mathcal{O}(2)$ 로 $\mathcal{O}(N)$ 으로 찾을 수 있을 것입니다.
하지만 이 방법으로는 $k$ 가 $N$ 에 비례하게 된다면 더이상 $\mathcal{O}(N)$ 으로 수행할 수 없게 됩니다. 예를 들어 중간값의 경우 $k$ 가 $\frac{N}{2}$ 입니다. 따라서, 후보군의 크기도 $\frac{N}{2}$ 이 되어야 하기 때문에, 후보군 업데이트 과정이 더이상 위 처럼 상수 시간이 될 수 없게 되서 이 방식으로는 $\mathcal{O}(N)$ 으로 중간값을 찾을 수 없습니다.
따라서 모든 $k$ 에 대해서 $\mathcal{O}(N)$ 으로 찾고 싶다면 다른 방법을 강구해야 합니다.
퀵 정렬에서 아이디어를 따오자
그렇다면 잠시 이전 아이디어는 접어두고, 한 번 퀵 정렬 방식에서 아이디어를 따와봅시다. 퀵 정렬의 코드를 살펴보면 아래와 같이 간단하게 생각할 수 있습니다.
# start 부터 end 까지 정렬한다 def quicksort(data, start, end): if start >= end : # 원소가 1 개거나 없는 경우 아무것도 안해도 된다. return # 피벗을 하나 고른다. pivot_pos = choose_pivot(data, start, end) # 파티션 후 피벗의 위치를 받는다. (파티션 후에 피봇의 위치가 바뀌므로 # 새로운 피벗 위치를 리턴한다.) pivot_pos = partition(data, start, end, pivot_pos) quicksort(data, start, pivot_pos - 1) # 피벗보다 작은 부분 quicksort(data, pivot_pos + 1, end) # 피벗보다 큰 부분
void quicksort(vector<T>& data, size_t start, size_t end) { if (start >= end) { return; } // 피벗을 하나 고른 뒤에 size_t pivot_pos = choose_pivot(data, start, end); // 피벗을 기준으로 파티션을 수행하고 (파티션 후에 피봇의 위치가 바뀌므로 // 새로운 피벗 위치를 리턴한다.) pivot_pos = partition(data, start, end, pivot_pos); // 피벗의 왼쪽을 정렬하고 quicksort(data, start, pivot_pos - 1); // 피벗의 오른쪽을 정렬합니다. quicksort(data, pivot_pos + 1, end); }
그렇다면 $k$ 번째 원소 찾기는 어떨까요? $k$ 번째 원소라는 뜻은, 정렬 하였을 때 자신에 앞에 원소가 $k - 1$ 개가 있다는 뜻입니다. 그렇다면
// 피벗을 기준으로 파티션을 수행하고 pivot_pos = partition(data, start, end, pivot_pos);
위 시점이 끝났을 때 피벗을 기준으로 왼쪽에는 피벗보다 작은애들, 오른쪽에는 피벗보다 큰 애들이 오게 됩니다. 마치 아래 그림과 같이 말이지요.
위 그림에서 한 가지 사실을 알아낼 수 있습니다. 바로 원소들을 정렬하였을 때 피벗이 정확히 맨 앞에서 부터 몇 번째에 위치하는지 입니다. 다시 말해 피벗 앞에 원소가 $m - 1$ 개 있다면 피벗은 $m$ 번째로 작은 원소가 됩니다!
다만 나머지 원소들에 대해서는 아무것도 단언할 수 있는 것이 없습니다. 피벗을 제외한 나머지 원소들은 피벗을 기준으로 작은애들은 왼쪽, 큰 애들은 오른쪽에 위치해 있을 뿐, 그들간의 상대적인 위치는 무작위라고 보면 됩니다.
만일 이 $m$ 이 우리가 원하는 $k$ 와 일치한다면 끝입니다. 하지만 $m$ 이 $k$ 와 일치하지 않는다면 어떨까요?
$k$ 가 $m$ 보다 크다고 해봅시다. 그렇다면 우리는 현재의 피벗보다 좀 더 큰 원소를 찾고 있는 것입니다. 따라서 해당 원소는 피벗 뒤에 위치하게 되겠지요. 따라서 다음 재귀 함수 호출은 피벗 뒤에 있는 원소들에만 적용하면 됩니다.
비슷한 이유로 $k$ 가 $m$ 보다 작다면 우리가 찾고 있는 원소는 피벗보다 앞에 있을 것입니다. 따라서 다음 재귀 함수 호출은 피벗 앞에 있는 원소들에만 수행하면 됩니다.
이 아이디어를 바탕으로 QuickSelect 알고리즘을 만들면 다음과 같습니다.
# 일단 피벗을 맨 마지막 원소로 항상 고른다. def choose_pivot(data, start, end): return end def partition(data, start, end, pivot_pos): # 우리의 partition 알고리즘은 피벗이 맨 마지막 원소라고 가정하므로 # pivot_pos 의 원소와 맨 마지막 원소의 위치를 바꾼다. data[end], data[pivot_pos] = data[pivot_pos], data[end] pivot = data[end] # 피봇은 마지막 원소로 current_small_loc = start # 빨간색 지시자 # i 는 검은색 지시자 for i in range(start, end + 1): if data[i] <= pivot: # swap 을 수행 data[i], data[current_small_loc] = data[current_small_loc], data[i] current_small_loc += 1 return current_small_loc - 1 # start 부터 end 까지 중 k 번째 원소를 찾는다. def quickselect(data, start, end, k): if start == end : return data[start] # 피벗을 하나 고른다. pivot_pos = choose_pivot(data, start, end) # 파티션 후 피벗의 위치를 받는다. (파티션 후에 피봇의 위치가 바뀌므로 # 새로운 피벗 위치를 리턴한다.) pivot_pos = partition(data, start, end, pivot_pos) if pivot_pos == k: # 빙고! return data[pivot_pos] elif pivot_pos < k: # 찾고자 하는 원소는 피벗 오른쪽에 있다. return quickselect(data, pivot_pos + 1, end, k) else: # 찾고자 하는 원소는 피벗 왼쪽에 있다. return quickselect(data, start, pivot_pos - 1, k) data = [3, 2, 5, 1, 7, 9, 6, 4, 8, 10] for i in range(10): # 1, 2, .., 10 까지 나올 것입니다. print(quickselect(data, 0, 9, i))
#include <algorithm> #include <iostream> #include <vector> template <typename T> // 일단 피벗을 맨 마지막 원소로 항상 고른다. size_t choose_pivot(const std::vector<T>& data, size_t start, size_t end) { return end; } template <typename T> size_t partition(std::vector<T>& data, size_t start, size_t end, size_t pivot_pos) { // 우리의 파티션 알고리즘은 피벗이 맨 마지막에 있다고 가정하므로, 고른 피벗을 // 맨 뒤로 옮긴다. std::iter_swap(data.begin() + end, data.begin() + pivot_pos); const auto& pivot = data[end]; size_t current_small_loc = start; // 검은색 지시자 // i 가 빨간색 지시자 역할을 한다. for (size_t i = start; i <= end; i++) { if (data[i] <= pivot) { std::swap(data[current_small_loc++], data[i]); } } return current_small_loc - 1; } template <typename T> T quickselect(std::vector<T>& data, size_t start, size_t end, size_t k) { if (start == end) { return data[start]; } // 피벗을 하나 고른다. size_t pivot_pos = choose_pivot(data, start, end); // 파티션 후 피벗의 위치를 받는다. pivot_pos = partition(data, start, end, pivot_pos); if (pivot_pos == k) { // 빙고! return data[pivot_pos]; } else if (pivot_pos < k) { // 찾고자 하는 원소는 피벗 오른쪽에 있다. return quickselect(data, pivot_pos + 1, end, k); } else { // 찾고자 하는 원소는 피벗 왼쪽에 있다. return quickselect(data, start, pivot_pos - 1, k); } } int main() { std::vector<int> data = {3, 10, 8, 5, 1, 4, 9, 2, 6, 7}; for (int k = 0; k < 10; k++) { std::cout << k + 1 << " 번 째 원소 : " << quickselect(data, 0, 9, k) << std::endl; } }
위와 같이 우리가 생각한 바를 그대로 코드로 옮기면 됩니다.
QuickSelect 의 시간 복잡도
QuickSelect 알고리즘의 시간 복잡도는 어떻게 알 수 있을까요? QuickSelect 에서 무언가가 일어나는 부분 은 바로 아래 줄에 해당합니다.
pivot_pos = partition(data, start, end, pivot_pos);
위 partition 함수의 경우 start 부터 end 까지의 원소들과 피벗을 한 번씩 비교하므로, 시간 복잡도가 파티션 하는 원소들의 수, 즉 $\mathcal{O}(\text{end} - \text{start})$ 가 됩니다.
그리고 이 파티션 하는 원소들의 개수는 이전 재귀 호출에서 피벗을 얼마나 잘 선택했냐에 달려 있지요. 이상적인 피벗은 데이터를 정확히 반 반으로 파티션 하는 피벗 - 즉 중간값(median)이 될 것입니다. 이 경우, end - start 의 크기가 다음 재귀 함수 호출 시에 절반으로 줄어들게 됩니다.
따라서 이상적인 QuickSelect 의 시간 복잡도는
$N + \frac{N}{2} + \frac{N}{4} + \cdots + 1 = N (1 + \frac{1}{2} + \frac{1}{4} + \cdots ) = 2N$
이므로, $\mathcal{O}(N)$ 만에 실행됩니다!
물론 피벗으로 중간값을 매번 고르는 일은 매우 어렵습니다. 그래도 적당히 좋은 피벗을 고른다면 $\mathcal{O}(N)$ 의 시간 복잡도를 실현할 수 있습니다. 예를 들어서 피벗이 대충 매번 1:3 의 비율로 파티션 한다고 치면 $N$ 다음에 그 다음 데이터셋의 크기는 $\frac{3}{4}N$ 이 되고 (물론 $\frac{1}{4}N$ 이 될 수 도 있겟지만, 최악의 상황을 가정합니다), 그 다음은 $(\frac{3}{4})^2N$ 순으로 진행됩니다. 따라서 전체 시간 복잡도는
$N (1 + \frac{3}{4} + (\frac{3}{4})^2 + \cdots) = N \frac{1}{1 - \frac{3}{4}} = 4N$
이 되므로 여전히 $\mathcal{O}(N)$ 으로 실행됩니다.
하지만 문제는 이 적당히 좋은 피벗 조차 고르는 것이 매우 힘든다는 것입니다. 최악의 경우에는 피벗으로 가장 큰 원소만을 고를 수 도 있는데 이렇게 된다면 전체 시간 복잡도는
$N + (N - 1) + (N - 2) + \cdots = \mathcal{O}(N^2)$
이 되어 매우 끔찍한 일이 발생하게 됩니다.
이렇게 최악의 시간 복잡도로 QuickSelect 알고리즘이 실행되는 것을 막기 위해서 사람들은 몇 가지 피벗 선택 방식을 제안하였습니다.
한 가지 방식은 피벗을 항상 무작위하게 택하는 것입니다. 이 경우 거의 100% $\mathcal{O}(N)$ 으로 실행됨을 보장할 수 있습니다. 문제는 같은 데이터셋에 대해서 QuickSelect 를 실행하더라도 매번 실행 속도가 달라진다는 점입니다. 따라서 표준 라이브러리 같은 곳에 사용하기에는 적합하지는 않습니다. 또한 무작위하게 피벗을 고르기 위해서는, 난수를 계속 생성해야 하는데 괜찮은 수준의 난수를 생성하는 일은 시간을 꽤나 잡아먹습니다. (덧붙여 피벗을 무작위 하게 고른다면 QuickSelect 의 시간 복잡도가 대략 $2n(1 + \ln 2 + o(1))$ 로 실행됨이 알려져 있습니다. 자세한 내용은 여기 에서 볼 수 있습니다.)
또 다른 방식으로는 셋에서 3 개의 원소를 고른 뒤에 (보통 맨 앞, 중간, 그리고 맨 뒤 원소) 이들 중 중간값을 피벗으로 택하는 방식입니다. 이를 통해 최악의 경우를 피할 수 있고, 특히 이미 정렬된 데이터 셋에 대해서도 매우 잘 작동합니다. 하지만, 사용자가 악의적으로 최악의 경우로 실행되는 데이터셋을 만들어낼 수 있습니다.
문제는 피벗을 고를 때 많은 시간을 투자할 수 없다는 점입니다. 이는 벼룩 잡으려다 초가삼간 태우는 격이지요. QuickSelect 가 $\mathcal{O}(N)$ 로 계속 동작하기 위해서는 피벗을 고르는 과정이 $\mathcal{O}(N)$ 으로 실행되어야만 합니다.
따라서 우리는 $\mathcal{O}(N)$ 의 시간 복잡도로 괜찮은 피벗 - 정확히 1 대 1 로 파티션 하지 못하더라도 일정 비율로 언제나 파티션 할 수 있는 피벗을 골라주는 알고리즘을 강구해야만 합니다.
Medians of medians
1979 년에 5 명의 걸출한 컴퓨터 과학자들 (Blum, Floyd, Pratt, Rivest, Tarjan) 에 의해 Medians of medians 라는 알고리즘이 발표되었습니다. 이 알고리즘은 이 컴퓨터 과학자들 이름의 앞글자를 다서 BFPRT 라고 불리기도 합니다.
Medians of medians 는 중간값을 정확히 찾지는 않지만 중간값과 근접한 값을 찾아주는 알고리즘 입니다. 정확히 말하자면, 데이터 셋에서 상위 30% 에서 70% 사이의 값을 언제나 찾아줍니다. 물론 이 정도만 되고 괜찮습니다. 왜냐하면 이 알고리즘을 QuickSelect 의 피벗 찾기에 적용할 경우, 셋의 크기가 매번 최소 $\frac{7}{10}$ 으로 줄어들기 때문이지요.
그렇다면 이 Medians of medians 알고리즘이 어떻게 작동하는지 알아보도록 하겠습니다.
기본적인 아이디어
Medians of medians 알고리즘의 바탕이 되는 아이디어는 바로 데이터 셋을 작은 그룹으로 쪼갠 다면, 각각의 그룹에서 중간값을 구하는 것은 상수 시간에 할 수 있다는 점입니다.
예를 들어서 아래와 같이 무작위로 정렬된 1 부터 100 까지의 수를 살펴봅시다.
이 때, 5 개씩 하나의 그룹으로 묶어서 생각해보도록 합시다. 위 경우, 같은 열에 있는 수들이 하나의 그룹에 들어갑니다. (예를 들어서 62, 70, 11, 1, 16).
각 그룹의 크기는 5 로 정해져 있기 때문에 각각의 그룹에서 중간값을 찾는 것은 상수 시간에 수행할 수 있습니다. 간단하게, 각각의 그룹을 모두 정렬했다고 칩시다. 그렇다면;
위와 같이 각 그룹에서 중간값들을 알아낼 수 있습니다. 위 그림에서 색칠된 부분이 각 그룹들의 중간값에 해당합니다.
그렇다면 위 과정 자체의 시간 복잡도는 얼마일까요? 일단 그룹의 총 개수는 $\frac{N}{5}$ 이고, 각 그룹을 정렬하는데 걸리는 시간은 $\mathcal{O}(1)$ 이므로, 위 과정은 $\mathcal{O}(N)$ 으로 수행됩니다.
여기서 Medians of medians 알고리즘의 중요 아이디어가 등장합니다. 과연, 저 색칠된 숫자들, 즉 각 그룹의 중간값들을 모은 집합의 중간값(median 들의 median!)은 실제 전체 데이터의 중간값와 얼마나 차이가 날까요?
위 경우 중간값들의 중간값은 55 이고, 실제 중간값은 50 이므로 거의 비슷합니다. 물론 이 경우 그냥 운이 좋아서라고 생각할 수 있기에 엄밀하게 우리가 구한 중간값들의 중간값이 실제 중간값과 얼마나 가까운지 계산해보도록 하겠습니다.
중간값들의 중간값 (Medians of medians)
먼저 우리가 찾은 각 그룹의 중간값들을 크기 순으로
$a_1 \le a_2 \le \cdots \le a_{\frac{n}{5}}$
라고 정의합시다. 그렇다면 이 중간값들 중 중간값은 당연히
$a_{\frac{n}{10}}$
이 되겠지요. 이제 $a_{\frac{n}{10}}$ 가 취할 수 있는 최소값을 생각해봅시다. 이를 위해서 $a_{\frac{n}{10}}$ 보다 작은 애들이 최소 몇 개 있는지 개수를 세보면 됩니다. 일단 $a_{\frac{n}{10}}$ 보다 작은 애들로 $a_1, a_2, \cdots, a_{\frac{n}{10} -1}$ 를 들을 수 있습니다.
그리고 $a_1$ 이 속해 있는 그룹에서, $a_1$ 이 중간값 이므로, $a_1$ 보다 2 개 있으므로, $a_{\frac{n}{10}}$ 보다 작은 애들이 $a_1$ 의 그룹에서 최소 3 개는 있게 됩니다. 이는 $a_{\frac{n}{10}}$ 가 속해 있는 그룹 까지 마찬가지 이므로, $a_{\frac{n}{10}}$ 보다 작은 애들의 개수는 최소
$\frac{n}{10} \times 3 = \frac{3n}{10}$
이 됩니다.
비슷한 논리로, $a_{\frac{n}{10}}$ 가 취할 수 있는 최대값은 $\frac{7n}{10}$ 임을 알 수 있습니다. 따라서, 우리가 중간값들의 중간값을 계산한다면, 해당 값은 전체 데이터의 상위 30% 에서 70% 사이에 항상 떨어진다는 것을 알 수 있습니다.
QuickSelect 알고리즘을 실행하기에 이 정도 성능만 보장되도 충분합니다. 왜냐하면 다루는 구간의 크기가 매 번 최소 $\frac{7}{10}$ 으로 줄어든다는 의미기 때문이지요.
그런데 문제는 중간값들의 후보 군에서 중간값을 찾아야 한다는 점입니다. 이를 어떻게 수행할 수 있을까요? 놀랍게도, 순환 논리의 함정에 빠진 것 같지만 중간값을 QuickSelect 알고리즘으로 찾아낼 수 있습니다.
아니 이게 무슨 말이여?
분명히 앞서 Medians of medians 알고리즘은 좋은 피벗을 찾는데 사용한다고 하였습니다. 좋은 피벗을 찾아야 하는 이유는 QuickSelect 알고리즘의 $\mathcal{O}(N)$ 성능을 보장하기 위해서였습니다. 그런데, 이 피벗을 찾기 위해서 다시 QuickSelect 를 사용해야 한다고요? 맞습니다. Medians of medians 알고리즘을 사용해서 피벗을 선택하는 과정은 아래와 같습니다.
def sort_and_get_median(data, start, end): data[start:end + 1] = sorted(data[start:end + 1]) return (start + end) // 2 def choose_pivot(data, start, end): # 데이터셋의 크기가 5 이하면 그냥 정렬해서 중간값을 계산한다. if end - start < 5: return sort_and_get_median(data, start, end - 1) # 5 개씩 끊어서 각각의 중간값을 구한 후, 앞으로 옮겨온다. current = start for i in range(start, end + 1, 5): med_pos = sort_and_get_median(data, i, min(i + 4, end)) data[current], data[med_pos] = data[med_pos], data[current] current += 1 # 그렇다면 start 부터 current - 1 까지 중간값들이 모여있게 된다. # current 부터 end 까지에는 나머지 데이터들이 들어있음! # 참고로 quickselect_pos 는 k 번째 원소의 값이 아니라 위치를 리턴한다. # 이는 choose_pivot 함수가 피벗의 위치를 리턴해야되기 때문. return quickselect_pos(data, start, current - 1, (current + start - 1) // 2)
template <typename T> T quickselect_pos(std::vector<T>& data, size_t start, size_t end, size_t k); template <typename T> size_t sort_and_get_median(std::vector<T>& data, size_t start, size_t end) { std::sort(data.begin() + start, data.begin() + end + 1); return (start + end) / 2; } template <typename T> size_t choose_pivot(std::vector<T>& data, size_t start, size_t end) { // 데이터 셋의 크기가 5 이하라면 그냥 정렬해서 중간값을 찾는다. if (end - start < 5) { return sort_and_get_median(data, start, end); } size_t current = start; for (size_t i = start; i <= end; i += 5) { // 데이터 셋을 크기가 5 인 그룹으로 쪼개서 각 그룹의 중간값을 찾는다. size_t med_pos = sort_and_get_median(data, i, std::min(i + 4, end)); // 각 그룹의 중간값을 맨 앞으로 가져온다. std::iter_swap(data.begin() + current, data.begin() + med_pos); current++; } return quickselect_pos(data, start, current - 1, (current + start - 1) / 2); }
choose_pivot 함수에서 바로 Medians of medians 알고리즘의 아이디어를 사용해서 피벗을 선택하는 과정을 수행하고 있습니다. 아래 부분에서 전체 구간을 5 개씩 쪼개서 각 그룹의 중간값을 계산하고 있는 과정을 수행합니다.
# 5 개씩 끊어서 각각의 중간값을 구한 후, 앞으로 옮겨온다. current = start for i in range(start, end + 1, 5): med_pos = sort_and_get_median(data, i, min(i + 4, end)) data[current], data[med_pos] = data[med_pos], data[current] current += 1
size_t current = start; for (size_t i = start; i <= end; i += 5) { // 데이터 셋을 크기가 5 인 그룹으로 쪼개서 각 그룹의 중간값을 찾는다. size_t med_pos = sort_and_get_median(data, i, std::min(i + 4, end)); // 각 그룹의 중간값을 맨 앞으로 가져온다. std::iter_swap(data.begin() + current, data.begin() + med_pos); current++; }
위와 같이 구간 안의 데이터셋을 5 개씩 끊어서 각각의 중간값들을 계산한 후 이들을 맨 앞으로 가져옵니다. 마치 아래 그림 처럼 말입니다.
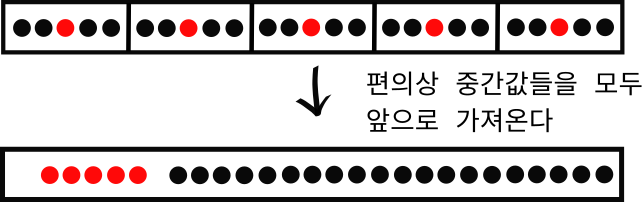
따로 앞으로 뺀 이유는 quickselect_pos 함수를 사용해서 쉽게 중간값을 계산하기 위함입니다. quickselect_pos 함수가 데이터를 구간의 형태로 받으므로, 중간값들이 한 군데에 모여 있어야만 합니다. 참고로 기존에 만들어놓았던 quickselect 함수가 아니라 quickselect_pos 함수를 사용하는 이유는 choose_pivot 함수가 피벗의 값이 아니라 피벗의 위치 를 리턴해야하기 때문입니다.
참고로 quickselect_pos 는 기존의 quickselect 에서 값 대신 그냥 위치만 리턴하도록 바꾸기만 하면 됩니다. 아래와 같이 말이지요.
def quickselect_pos(data, start, end, k): if start == end: return start # 피벗을 하나 고른다. pivot_pos = choose_pivot(data, start, end) # 파티션 후 피벗의 위치를 받는다. (파티션 후에 피봇의 위치가 바뀌므로 # 새로운 피벗 위치를 리턴한다.) pivot_pos = partition(data, start, end, pivot_pos) if pivot_pos == k: # 빙고! return pivot_pos elif pivot_pos < k: # 찾고자 하는 원소는 피벗 오른쪽에 있다. return quickselect_pos(data, pivot_pos + 1, end, k) else: # 찾고자 하는 원소는 피벗 왼쪽에 있다. return quickselect_pos(data, start, pivot_pos - 1, k)
template <typename T> T quickselect_pos(std::vector<T>& data, size_t start, size_t end, size_t k) { if (start == end) { return start; } // 피벗을 하나 고른다. size_t pivot_pos = choose_pivot(data, start, end); // 파티션 후 피벗의 위치를 받는다. pivot_pos = partition(data, start, end, pivot_pos); if (pivot_pos == k) { // 빙고! return pivot_pos; } else if (pivot_pos < k) { // 찾고자 하는 원소는 피벗 오른쪽에 있다. return quickselect_pos(data, pivot_pos + 1, end, k); } else { // 찾고자 하는 원소는 피벗 왼쪽에 있다. return quickselect_pos(data, start, pivot_pos - 1, k); } }
따라서 전체 코드는 아래와 같습니다.
def sort_and_get_median(data, start, end): data[start:end + 1] = sorted(data[start:end + 1]) return (start + end) // 2 def choose_pivot(data, start, end): if end - start < 5: return sort_and_get_median(data, start, end - 1) # 5 개씩 끊어서 각각의 Median 을 구한 후, 맨 앞으로 옮겨온다. current = start for i in range(start, end + 1, 5): med_pos = sort_and_get_median(data, i, min(i + 4, end)) data[current], data[med_pos] = data[med_pos], data[current] current += 1 # 그렇다면 start 부터 current - 1 까지 median 들이 모여있게 된다. # current 부터 end 까지에는 나머지 데이터들이 들어있음! return quickselect_pos(data, start, current - 1, (current + start - 1) // 2) def partition(data, start, end, pivot_pos): # 우리의 partition 알고리즘은 피벗이 맨 마지막 원소라고 가정하므로 # pivot_pos 의 원소와 맨 마지막 원소의 위치를 바꾼다. data[end], data[pivot_pos] = data[pivot_pos], data[end] pivot = data[end] # 피봇은 마지막 원소로 current_small_loc = start # 빨간색 지시자 # i 는 검은색 지시자 for i in range(start, end + 1): if data[i] <= pivot: # swap 을 수행 data[i], data[current_small_loc] = data[current_small_loc], data[i] current_small_loc += 1 return current_small_loc - 1 def quickselect_pos(data, start, end, k): if start == end: return start # 피벗을 하나 고른다. pivot_pos = choose_pivot(data, start, end) # 파티션 후 피벗의 위치를 받는다. (파티션 후에 피봇의 위치가 바뀌므로 # 새로운 피벗 위치를 리턴한다.) pivot_pos = partition(data, start, end, pivot_pos) if pivot_pos == k: # 빙고! return pivot_pos elif pivot_pos < k: # 찾고자 하는 원소는 피벗 오른쪽에 있다. return quickselect_pos(data, pivot_pos + 1, end, k) else: # 찾고자 하는 원소는 피벗 왼쪽에 있다. return quickselect_pos(data, start, pivot_pos - 1, k) # start 부터 end 까지 정렬한다 def quickselect(data, start, end, k): if start == end: return data[start] # 피벗을 하나 고른다. pivot_pos = choose_pivot(data, start, end) # 파티션 후 피벗의 위치를 받는다. (파티션 후에 피봇의 위치가 바뀌므로 # 새로운 피벗 위치를 리턴한다.) pivot_pos = partition(data, start, end, pivot_pos) if pivot_pos == k: # 빙고! return data[pivot_pos] elif pivot_pos < k: # 찾고자 하는 원소는 피벗 오른쪽에 있다. return quickselect(data, pivot_pos + 1, end, k) else: # 찾고자 하는 원소는 피벗 왼쪽에 있다. return quickselect(data, start, pivot_pos - 1, k)
#include <algorithm> #include <iostream> #include <random> #include <vector> template <typename T> T quickselect_pos(std::vector<T>& data, size_t start, size_t end, size_t k); template <typename T> size_t sort_and_get_median(std::vector<T>& data, size_t start, size_t end) { std::sort(data.begin() + start, data.begin() + end + 1); return (start + end) / 2; } template <typename T> size_t choose_pivot(std::vector<T>& data, size_t start, size_t end) { // 데이터 셋의 크기가 5 이하라면 그냥 정렬해서 중간값을 찾는다. if (end - start < 5) { return sort_and_get_median(data, start, end); } size_t current = start; for (size_t i = start; i <= end; i += 5) { // 데이터 셋을 크기가 5 인 그룹으로 쪼개서 각 그룹의 중간값을 찾는다. size_t med_pos = sort_and_get_median(data, i, std::min(i + 4, end)); // 각 그룹의 중간값을 맨 앞으로 가져온다. std::iter_swap(data.begin() + current, data.begin() + med_pos); current++; } return quickselect_pos(data, start, current - 1, (current + start - 1) / 2); } template <typename T> size_t partition(std::vector<T>& data, size_t start, size_t end, size_t pivot_pos) { // 우리의 파티션 알고리즘은 피벗이 맨 마지막에 있다고 가정하므로, 고른 피벗을 // 맨 뒤로 옮긴다. std::iter_swap(data.begin() + end, data.begin() + pivot_pos); const auto& pivot = data[end]; size_t current_small_loc = start; // 검은색 지시자 // i 가 빨간색 지시자 역할을 한다. for (size_t i = start; i <= end; i++) { if (data[i] <= pivot) { std::swap(data[current_small_loc++], data[i]); } } return current_small_loc - 1; } template <typename T> T quickselect_pos(std::vector<T>& data, size_t start, size_t end, size_t k) { if (start == end) { return start; } // 피벗을 하나 고른다. size_t pivot_pos = choose_pivot(data, start, end); // 파티션 후 피벗의 위치를 받는다. pivot_pos = partition(data, start, end, pivot_pos); if (pivot_pos == k) { // 빙고! return pivot_pos; } else if (pivot_pos < k) { // 찾고자 하는 원소는 피벗 오른쪽에 있다. return quickselect_pos(data, pivot_pos + 1, end, k); } else { // 찾고자 하는 원소는 피벗 왼쪽에 있다. return quickselect_pos(data, start, pivot_pos - 1, k); } } template <typename T> T quickselect(std::vector<T>& data, size_t start, size_t end, size_t k) { if (start == end) { return data[start]; } // 피벗을 하나 고른다. size_t pivot_pos = choose_pivot(data, start, end); // 파티션 후 피벗의 위치를 받는다. pivot_pos = partition(data, start, end, pivot_pos); if (pivot_pos == k) { // 빙고! return data[pivot_pos]; } else if (pivot_pos < k) { // 찾고자 하는 원소는 피벗 오른쪽에 있다. return quickselect(data, pivot_pos + 1, end, k); } else { // 찾고자 하는 원소는 피벗 왼쪽에 있다. return quickselect(data, start, pivot_pos - 1, k); } } int main() { std::vector<int> data; data.reserve(10000); for (int i = 1; i <= 10000; i++) { data.push_back(i); } std::random_device rd; std::mt19937 g(rd()); for (int i = 0; i < 10; i++) { // 데이터를 랜덤하게 섞는다. std::shuffle(data.begin(), data.end(), g); // 매번 5000 이 나와야 한다. std::cout << "중간값 : " << quickselect(data, 0, 9999, 4999) << std::endl; } }
Medians of medians 를 사용한 QuickSelect 의 시간 복잡도
그렇다면 Medians of medians 알고리즘을 사용한 QuickSelect 의 시간 복잡도가 어떻게 될지 생각해봅시다. 왠지 피벗을 고르는 과정에서 QuickSelect 를 재귀적으로 호출하였기에, 배보다 배꼽이 커지지는 않았는지 걱정할 수 도 있는데, 한 번 계산해보도록 합시다. (수학적으로 조금 더 엄밀한 접근은 이 알고리즘을 제안한 사람 중 한 명인 Rivest 의 강의 노트에서 확인할 수 있습니다.)
편의상 $n$ 개의 데이터를 받는 QuickSelect 의 시간 복잡도를 $T(n)$ 이라고 정의합시다.
먼저 choose_pivot 함수의 호출하는 부분의 시간 복잡도는 어떻게 될까요? 앞서 이야기 했듯이 데이터셋을 5 개씩 총 $\frac{n}{5}$ 개로 쪼갠 후 각각을 정렬하는데 $\mathcal{O}(1)$ 이 걸리므로 $\mathcal{O}(n)$ 이 걸릴 것입니다.
그렇다면 $\frac{n}{5}$ 개의 중간값들 중에서 중간값을 찾는 과정은요? 이를 위해서 우리는 QuickSelect 함수를 호출하였죠! 따라서 이 과정은 $T(\frac{n}{5})$ 로 수행됩니다.
자 이렇게 해서 choose_pivot 함수가 끝난 다음에는 quickselect 함수로 돌아오게 됩니다. 위에서 증명하였듯이 우리가 고른 피벗은 매우 훌륭해서 파티션 시에 최소 3 대 7 로 쪼개게 됩니다. 따라서 다음 재귀 호출 시에 데이터 셋의 크기는 아무리 커도 $\frac{7n}{10}$ 이 될 것입니다. 또한 파티션 자체는 $\mathcal{O}(n)$ 으로 수행되지요.
결과적으로 우리는 아래와 같은 관계식을 얻을 수 있게 됩니다.
$T(n) = \mathcal{O}(n) + T(\frac{n}{5}) + T(\frac{7n}{10})$
흠 그렇다면 위 관계식을 어떻게 풀어서 $T(n)$ 을 $n$ 에 대한 식으로 나타낼 수 있을까요? 편의상 $\mathcal{O}(n)$ 을 big-O 의 정의에 따라 어떠한 $a$ 가 있어서 $\mathcal{O}(n) \le a \cdot n$ 을 만족한다고 해봅시다. 그렇다면 위 식은
$T(n) \le a\cdot n + T(\frac{n}{5}) + T(\frac{7n}{10})$
을 만족하게 됩니다. 이제, 우리는 귀납법으로 어떠한 $c > 10a$ 가 있어서 $T(n) \le c\cdot n$ 을 만족함을 보이도록 하겠습니다.
먼저 귀납 가정으로 $n$ 보다 작은 모든 $k < n$ 에 대해 $T(k) \le c \cdot k$ 이 성립함을 가정합시다. 그러면 이제 $n$ 일 때만 보여주면 됩니다. 그런데 귀납 가정에 따라
$T(n) \le a \cdot n + c \frac{n}{5} + c\frac{7n}{10} = n (\frac{9c}{10} + a)$
가 성립하는데, 앞서 $c > 10a$ 로 정의하였으므로
$T(n) \le n (\frac{9c}{10} + a) \le n (\frac{9c}{10} + \frac{c}{10}) = c \cdot n$
이 되어서 귀납법이 성립하게 됩니다. 따라서 우리는 $T(n) = \mathcal{O}(n)$ 임을 알 수 있습니다.
따라서 이 Medians of medians 를 사용한 QuickSelect 의 시간 복잡도는 놀랍게도 $\mathcal{O}(n)$ 로 보장됩니다. 최악의 경우에도 말입니다. 멋지지 않나요?
그래서 실제로 Medians of medians 를 쓰는가?
Medians of medians 알고리즘을 사용하는 QuickSelect 는 최악의 경우에도 $\mathcal{O}(n)$ 이 보장되지만 실제로는 Medians of medians 알고리즘 만 사용해서 k 번째 원소를 찾는 알고리즘을 구현하는 일은 거의 없습니다. 왜냐하면 아무리 $\mathcal{O}(n)$ 이라도 숨어 있는 상수항이 너무 크기 때문입니다.
C++ 표준 라이브러리의 nth_element 함수의 경우 IntroSelect 라는 방식을 사용하는데, 이는 피벗을 고를 때 원소 3 개를 골라서 그 중 중간값을 피벗으로 고르는 방식을 사용하다가, 이 방식으로 진행이 너무 더디다면 Medians of medians 알고리즘을 사용하는 방식으로 바뀌는 혼합된 방식으로 사용합니다.
비록 Medians of medians 알고리즘을 직접 사용할 일은 거의 없지만 그 안에 녹아 있는 아이디어는 매우 기똥차며 훗날 다른 알고리즘들에도 비슷한 아이디어가 많이 적용되었습니다.
그렇다면 이번 강좌는 여기에서 마치도록 하겠습니다.
생각 해보기
문제 1
Medians of medians 알고리즘에서 5 개의 원소를 한 그룹으로 만들었습니다. 만약에 이 그룹의 크기를 3 개의 원소로 줄이면 어떤 문제가 생길까요? 반대로 7 개로 늘린다면 어떨까요?
댓글을 불러오는 중입니다..