모두의 코드
모두의 알고리즘 - 2 - 2. 정렬 알고리즘의 꽃 - 퀵 소트(Quicksort)
안녕하세요 여러분! 이번 강좌에서는 정렬 알고리즘을 사용하는데 가장 보편적으로 사용되는 퀵 정렬 (Quicksort) 방식에 대해 알아보도록 하겠습니다. 사실 이름만 봐도 왠지 빠를 것 같다는 느낌이 들죠?
퀵 정렬 (Quicksort)
앞서 거품 정렬 방식이 느린 이유는 필요 없는 비교를 자주 수행하기 때문이라 했었습니다. 예를 들어서
$a_1, a_2, a_3$
와 같은 데이터가 있을 때,
우리가 이미 $a_1 < a_2$ 이고 $a_2 < a_3$ 이라는 사실을 알았다면, 굳이 $a_1$ 과 $a_3$ 을 비교하지 않고도 $a_1 < a_3$ 임을 알 수 있기 때문이지요.
그렇다면, 만약에 어떤 데이터를 기준으로 왼쪽에는 기준보다 작은애들, 오른쪽에는 기준보다 큰 애들만 모아 놓으면 어떨까요? 예를 들어서 아래와 같이 3, 10, 8, 5, 1, 4, 9, 2, 6, 7 와 같은 데이터가 있다고 해봅시다.
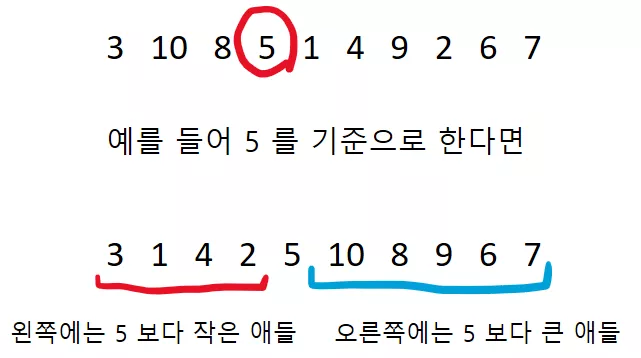
만약에 5 를 기준으로 왼쪽에는 5 보다 작은애들, 오른쪽에는 5 보다 큰 애들로 모아두면 어떨까요?
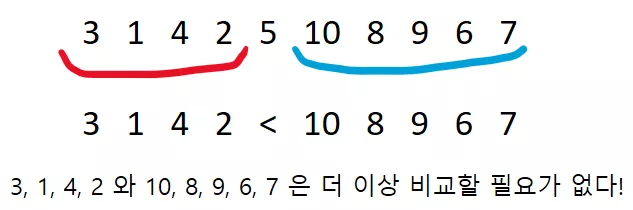
그렇다면 이제 더이상 왼쪽 부분의 원소들과 오른쪽 부분의 원소들의 크기 비교는 할 필요가 없게 됩니다! 왜냐하면 이미 왼쪽 부분은 5 보다 작은 애들을 모아놓았고, 오른쪽 부분에는 5 보다 큰 애들을 모아놓은 것이기 때문이지요.
이와 같이 어떠한 원소를 기준으로 한쪽에는 작은애들, 한쪽에는 큰 애들을 모아놓는 작업을 파티션(partition) 한다고 부릅니다.
파티션 한 후에, 왼쪽 부분과 오른쪽 부분만 각각 따로 정렬해주면 끝입니다!
그렇다면 파티션을 어떻게?
이로써 정렬을 할 수 있는 것일까요? 아직 좋아하기는 조금 이릅니다. 아래 두 가지 질문에 대해 생각해봐야 합니다.
기준점 을 어떻게 잡아야 할까요?
파티션을 어떻게 하면 빠르게 할 수 있을까요?
먼저 기준점(영어로는 피벗 - pivot 이라고 부릅니다)을 어떻게 잡아야 할까요? 어쩌다가 기준점을 배열에서 가장 큰 원소로 잡았다고 해봅시다.
위 경우 10 을 피벗으로 잡았다면 10 이 맨 뒤에 오고 그 앞에 1 부터 9 까지 오게 됩니다. 결과적으로 보았을 때, 10 의 위치만 찾았을 뿐 어차피 앞의 원소들을 다시 정렬해야 되겠죠. 말 그대로 최악의 경우 가 된 것입니다.
가장 이상적인 상황은 피벗으로 중간값(median)을 골라서 원소들을 최대한 균등하게 배분하는 것입니다. 앞서 5 를 골랐을 때 골고루 5 개와 4 개로 나눌 수 있었지요.
하지만 중간값을 찾는 것은 꽤나 어렵습니다. 오히려 중간값을 굳이 피벗으로 고르려다 배보다 배꼽이 커지는 일이 발생할 수 도 있지요 (중간값 찾기는 꽤나 어려운 문제입니다).
따라서 중간값을 택하는 방향 보다는 최악의 경우를 피하는 방식으로 피벗을 고르게 됩니다. 이를 위해서 보통 앞의 3 개의 원소의 중간값을 택하는 식으로 합니다.
이제 그렇다면 파티션을 어떻게 하면 빠르게 할 수 있을까요?
가장 단순하게 파티션 하기
여러분이라면 어떻게 파티션을 하실 건가요? 보통 어떠한 문제에 접근할 때 가장 먼저 해야할 방법은 가장 단순한 방법 으로 문제를 접근하는 것입니다. 이를 더 빠르게 하는 것은 나중에 할 고민이지요.
편의상 맨 뒤에 있는 원소가 피벗이라고 해봅시다. 그 후에, 새로운 메모리를 할당 받아서, 피벗 보다 작은 원소는 앞에서 부터 가져다 놓고, 피벗 보다 큰 원소는 뒤에서 부터 채워놓으면 됩니다. 아래 그림을 보면 이해가 더 잘될 것입니다.
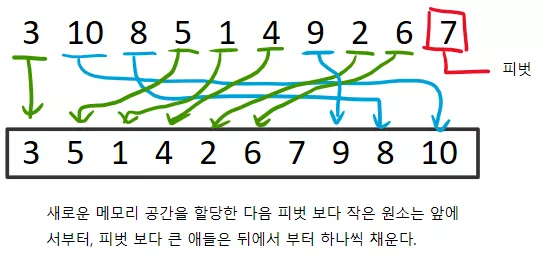
그리고 파티션 후의 피벗의 위치는, 마지막 원소가 들어간 위치가 되겠네요 (피벗이 맨 뒤에 있다고 했으므로). 이 과정을 코드로 나타내면 다음과 같습니다.
# data 의 start 부터 end 까지의 원소들을 파티션한 후 pivot 의 위치를 리턴한다. def partition(data, start, end): pivot = data[end] # 피봇은 마지막 원소로 # 일단 크기 (end - start + 1) 의 배열을 준비한다. # (start ~ end 까지 원소들을 포함해야 하므로) partitioned_data = [0] * (end - start + 1) left = 0 # 피벗보다 작은 애들 넣을 위치 right = end - start # 피봇 보다 큰 애들 넣을 위치 for i in range(start, end + 1): if data[i] <= pivot: partitioned_data[left] = data[i] left += 1 else: partitioned_data[right] = data[i] right -= 1 # 파티션 된 애들을 원래 data 로 복사한다. for i in range(end - start + 1): data[i + start] = partitioned_data[i] # 결국 피봇이 들어가는 위치는 right 가 가리키고 있는 위치이다. # (왜 인지 생각해보세요!) return right
#include <algorithm> #include <iostream> #include <vector> using namespace std; template <typename T> size_t partition(vector<T>& data, size_t start, size_t end) { const auto& pivot = data[end]; vector<T> partitioned_data(end - start + 1); size_t left = 0; size_t right = end - start; for (size_t i = start; i <= end; i++) { if (data[i] <= pivot) { partitioned_data[left++] = data[i]; } else { partitioned_data[right--] = data[i]; } } for (size_t i = 0; i <= end - start; i++) { data[i + start] = partitioned_data[i]; } return right; } int main() { vector<int> data = {3, 10, 8, 5, 1, 4, 9, 2, 6, 7}; cout << "피봇 위치 : " << partition(data, 0, data.size() - 1) << endl; cout << "파티션 후 ---" << endl; for (int num : data) { cout << num << " "; } }
그렇다면 위 partition 함수의 작동 속도는 어떨까요? 위 함수의 시간 복잡도는 가운데 이는 루프에서 결정되는데, 이 루프가 start 부터 end 까지 쭈르륵 스캔하는 것이기 때문에 $O(n)$ 이 될 것입니다. ($n$ 은 파티션 하는 데이터의 크기)
하지만 위 구현은 한 가지 문제가 있는데, 매 partition 마다 $n$ 크기의 메모리를 새로 할당해야 된다는 점입니다. 물론 $n$ 크기의 메모리를 할당하는 작업도 $O(n)$ 이여서 전체 시간 복잡도 Big-O 표현에는 차이가 없지만, 실제 프로그램 속도는 꽤나 느려질 것입니다.
재미있게도, partition 작업을 추가적인 메모리 할당 없이 전달된 메모리 자체에서 해결할 수 있습니다. 이와 같이 부수적인 메모리 할당 없이 주어진 메모리 상에서 작업을 수행할 수 있는 것을 in-place 라고 합니다. 퀵 소트를 통해 in-place 정렬을 할 수 있습니다.
in-place 로 partition 하기
앞서 단순하게 파티션 하는 방식으로는 in-place 파티션을 할 수 없습니다. 왜냐하면 피벗 보다 큰 애들을 뒤에다 쓰게 된다면, 해당 자리에 있던 원소를 덮어쓰기 때문이지요. 따라서 그 자리에 있던 원소를 제대로 처리할 수 없게 됩니다.
하지만 만약에 피벗 보다 큰 애들을 그냥 그 자리에 놔두면 어떨까요? 그 대신에, 피벗 보다 작은 애들을 앞에 옮길 때, 해당 위치에 있는 원소와 자리를 바꾸면 됩니다!
무슨 말인지 이해가 안가신다고요? 아래 자세한 과정을 살펴보도록 합시다.
일단 아래와 같이 두 개의 지시자를 생각해봅시다. 하나는 현재 어떤 원소를 확인하는지 가리키는 지시자 이고 (빨간색), 하나는 어느 위치에 피벗 보다 작은 애가 올 것인지를 가리키고 있습니다 (검은색).
이 때 파티션 하는 방법은 다음과 같습니다.
현재 확인하는 원소가 피벗 보다 작으면 피벗 보다 작은 애가 올 위치에 있는 원소와 위치를 서로 바꾼다음(swap) 검은색 지시자를 한 칸 전진 시킨다. (즉 그 다음 피벗보다 작은 원소는 그 뒤에 와야되기 때문)
빨간색 지시자를 한 칸 전진 시킨다.
그렇다면 위 상황에서 다음 단계의 모습은 어떨까요? 현재 확인하는 원소 (3) 이 피벗 (7) 보다 작기 때문에 빨간색 지시자가 가리키는 원소와 검은색 지시자가 가리키는 원소를 서로 바꾼 후, 검은색 지시자를 한 칸 전진 시키면 되겠지요.
위 경우 빨간색과 검은색 지시자가 같은 원소를 가리키고 있으므로, 3 은 그대로 있고 검은색 지시자만 한 칸 앞으로 가게 됩니다.
그 후 이제 다음 원소를 살펴봅시다.
10 은 7 보다 크기 때문에 다시 빨간색 지시자가 한 칸 전진합니다.
8 역시 7 보다 크기 때문에 또 한 칸 전진합니다.
이제 다시 피벗 보다 작은 것이 나왔습니다. 5 가 7 보다 작기 때문에, 현재 피벗 보다 작은 원소가 가야하는 위치에 서로 swap 하면 됩니다. 그 후 다시 검은색 지시자를 한 칸 전진 시키면 아래와 같이 됩니다. (10 과 5 가 swap 된 것을 볼 수 있습니다)
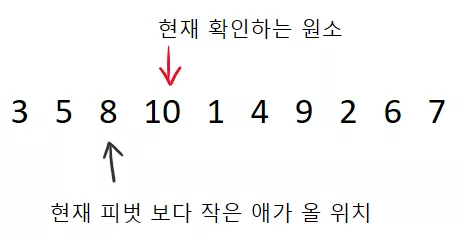
그리고 빨간색 지시자를 한 칸 전진 시킵니다. 한 가지 재미있는점은 swap 된 원소를 굳이 다시 확인할 필요는 없습니다. 왜냐하면, swap 되었단 뜻은 피벗 보다 커서 그 앞에 남아 있었기 때문 이죠.
1 의 경우 마찬간지로 7 보다 작습니다. 따라서 swap 후에 빨간색 지시자와 검은색 지시자를 전진시키면;
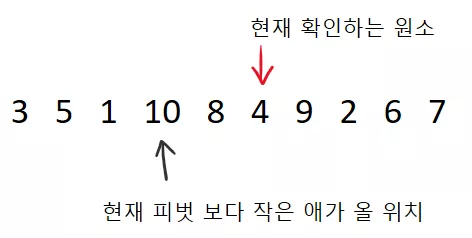
이 됩니다. 4 역시 7 보다 작으므로 swap 후 빨간색 및 검은색 지시자 전진 하면;
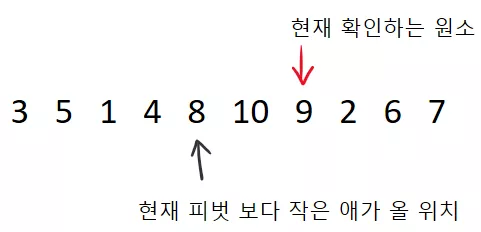
가 됩니다. 쭉쭉쭉 하게 된다면, 아래와 같이 될 것입니다.
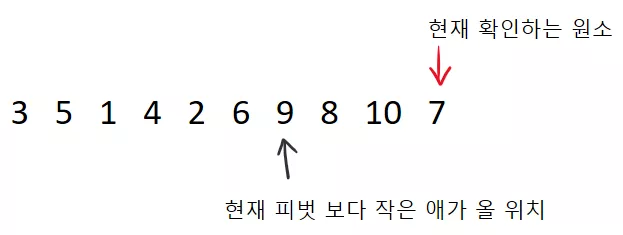
그리고 마지막으로 피벗을 검은색 지시자가 가리키는데 가져다 놓으면 끝입니다! 그리고 그 위치가 파티션 후의 피벗의 위치가 되겠지요.
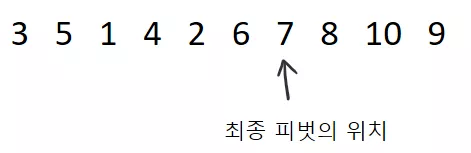
왜 위와 같은 방식으로 파티션을 할 수 있는지 이해가 가시나요? 검은색 지시지가 다음 피벗보다 작은 원소가 올 위치를 계속 파악하고 있기에 성공적으로 파티션을 수행할 수 있었습니다. 이 과정을 코드로 나타내면 다음과 같습니다.
# data 의 start 부터 end 까지의 원소들을 파티션한 후 pivot 의 위치를 리턴한다. def partition(data, start, end): pivot = data[end] # 피봇은 마지막 원소로 current_small_loc = start # 검은색 지시자 # i 는 빨간색 지시자 for i in range(start, end + 1): if data[i] <= pivot: # swap 을 수행 data[i], data[current_small_loc] = data[current_small_loc], data[i] current_small_loc += 1 return current_small_loc - 1
template <typename T> size_t partition(vector<T>& data, size_t start, size_t end) { const auto& pivot = data[end]; size_t current_small_loc = start; // 검은색 지시자 // i 가 빨간색 지시자 역할을 한다. for (size_t i = start; i <= end; i++) { if (data[i] <= pivot) { swap(data[current_small_loc++], data[i]); } } return current_small_loc - 1; }
전체 퀵 소트 알고리즘
자 그럼 전체 퀵 소트 알고리즘을 구현해봅시다. 일단 파티션 함수를 잘 구현하였다면 사실 나머지는 크게 어렵지 않습니다.
# start 부터 end 까지 정렬한다 def quicksort(data, start, end): if start >= end : # 원소가 1 개거나 없는 경우 아무것도 안해도 된다. return # 파티션 후 피벗의 위치를 받는다. pivot_pos = partition(data, start, end) quicksort(data, start, pivot_pos - 1) # 피벗보다 작은 부분 quicksort(data, pivot_pos + 1, end) # 피벗보다 큰 부분
template <typename T> void quicksort(vector<T>& data, size_t start, size_t end) { if (start >= end) { return; } size_t pivot_pos = partition(data, start, end); quicksort(data, start, pivot_pos - 1); quicksort(data, pivot_pos + 1, end); }
매우 간단하지요? 하지만 아직 몇 가지 문제들이 남아 있습니다. 앞서 말했듯이 운이 나쁘다면, 피벗을 잘못 골라서 시간 복잡도가 $O(n^2)$ 이 나올 수 있습니다. 예를 들어서 이미 정렬되어 있는 배열 - 예컨대 [1,2, 3, 4] 를 정렬하는 경우를 생각해봅시다.
이 경우 위 partition 은 맨 마지막 원소를 택하기 때문에 4 가 피벗으로 택해지고, 위 경우 [1,2,3] 과 [4] 로 나뉘게 됩니다. 다시 [1,2,3] 의 경우 3 이 피벗으로 택해지기 때문에 [1,2] 와 [3] 으로 나뉘고, 결국 [1,2] 는 [1] 과 [2] 로 나뉘게 됩니다.
이 과정에서 파티션 시에 총 $4 + 3 + 2 + 1$ 번의 연산을 하기 때문에 결과적으로 전체 수행 시간은 $O(n^2)$ 이 됩니다 ($\because n + (n - 1) + \cdots + 2 + 1 = n(n+1)/2 = O(n)$).
이를 해결하기 위해선 여러가지 방법이 있는데 가장 쉬운 방법으로는 3 개의 원소를 확인한 뒤에, 그 중 중간 원소를 피벗으로 택하는 것입니다. 이 경우 최소한 최악의 경우를 피할 수 있지요. 물론, 우리의 partition 함수는 맨 뒤에 피벗이 있다고 가정하므로, 피벗을 택한 뒤에, 맨 뒤의 원소와 바꿔치기 하면 됩니다.
실제로 리눅스 C++ 라이브러리의 경우 피벗을 첫번째, 가운데 원소, 마지막 원소 중 중간값을 피벗으로 택합니다. (여기 에서 2320 번째 줄을 보시면 됩니다. __move_median_first 함수가 인자로 전달된 세 개의 값들 중 중간값을 앞으로 가져옵니다)
다른 한 가지 방법으로는 무작위로 피벗을 택하는 것입니다. 물론 실제 구현에서는 잘 사용되지는 않 습니다. 왜냐하면 랜덤으로 수를 구하는 것이 꽤나 시간을 잡아먹기 때문입니다.
퀵 소트의 또 다른 장점으로 우수한 공간 복잡도를 꼽을 수 있습니다. 병합 정렬의 경우 merge 를 위해 전체 데이터 만큼의 메모리를 할당해야 하지만 (공간 복잡도 $\mathcal{O}(n)$), 퀵 소트의 경우 모든 연산이 in-place 로 이루어지므로, 데이터를 위해서 굳이 부가적인 메모리를 할당할 수 없습니다.
하지만 재귀적으로 함수가 호출 되기 때문에 퀵소트의 경우 $\mathcal{O}(\log n)$ 만큼의 공간 복잡도를 필요로 합니다. (물론 병합 정렬도 마찬가지 이지만 $\mathcal{O}(n)$ 이 더 크므로 big-O 에는 표현되지 않습니다.)
퀵 소트의 정확한 시간 복잡도
퀵 소트의 시간 복잡도를 구하는 것은 꽤나 복잡합니다. 만약에 피벗이 언제나 절반으로 데이터를 나눈다면
$T(n) = 2 T(\frac{n}{2}) + O(n)$
와 같은 관계식을 만족해서 $T(n) = O(n \log n)$ 임을 쉽게 알 수 있지만, 실제로는 피벗이 항상 운 좋게 절반으로 나눌 수 없기 때문에 위와 같은 관계식을 항상 만족할 수 없죠.
심지어, 매 partition 에서 피벗이 일정하게 데이터를 나누는 것도 아닙니다. 어떨 때에는 운이 좋아서 절반으로 나눌 수 있지만, 운이 나쁘다면 대충 1 : 9 쯤 으로 나눌 수 도 있겠지요. 따라서 정확한 관계식을 구하는 것은 거의 불가능 하다고 볼 수 있습니다.
하지만, 재미있게도 피벗을 무작위로 택한다면, 퀵 소트의 평균 시간 복잡도가 정확히 $O(n\log n)$ 임을 증명 할 수 있습니다.
이를 위해 몇 가지 알아야 할 수학적 사실들이 있습니다.
기대값
수학에서 기대값(expected value) 이란, 어떠한 사건 평균적으로 몇 번 일어나는지를 나타냅니다. 예를 들어서 어떠한 슬롯 머신이 있는데 $\frac{1}{2}$ 확률로 100 원을 잃고, $\frac{1}{3}$ 확률로 50 원을 벌고, $\frac{1}{6}$ 확률로 200 원을 준다면, 내가 이 슬롯 머신을 돌림으로써 벌 수 있는 금액은
$\frac{1}{2} \cdot (-100) + \frac{1}{3} \cdot 50 + \frac{1}{6} \cdot 200 = 0$
0 원이 되겠습니다 (되게 착한 카지노 인가 봅니다..).
엄밀히 말해서 어떠한 사건 $x_i$ 가 일어날 확률이 $p(x_i)$ 라면 기대값은 다음과 같이 정의됩니다.
$E[X] = \sum_{i} p(x_i) x_i$
한 가지 재미 있는 점은 기대값이 선형 이라는 점 입니다(Linearity of expectation). 이 말이 무슨 말이냐면, 어떠한 확률 변수 $X, Y$ 가 독립이냐 아니냐에 상관 없이 아래와 같은 관계식을 항상 만족합니다.
$E[X + Y] = E[X] + E[Y]$
이는 기대값에서 가장 자주 쓰이는 특성입니다. 이 특성이 중요한 이유는 분산과 같은 다른 값들은 선형이 아니기 때문에, $X$ 와 $Y$ 가 독립사건이 아닐 때 잘 계산해야 되겠지만, 기대값은 선형이기에 어떠한 두 확률 변수가 합쳐져 있다면 그냥 각각 구한 다음 더해주면 됩니다.
그래서 퀵소트는?
자 그렇다면 이 퀵소트 문제를 어떻게 접근할까요? 시간 복잡도는 결국 어떤 두 원소의 비교를 몇 번 하느냐에 달려 있습니다. 또한, 이 퀵소트를 잘 생각해보면 알겠지만, 임의의 두 원소는 최대 1 번 비교 합니다.
왜냐고요? 일단 두 원소가 언제 비교되는지 생각해봅시다. 위 퀵소트 과정을 다시 살펴보자면 원소의 비교는 딱
// i 가 빨간색 지시자 역할을 한다. for (size_t i = start; i <= end; i++) { if (data[i] <= pivot) { // <--- 원소의 비교! swap(data[current_small_loc++], data[i]); } }
저 피봇와 원소를 비교하는 지점에서만 발생하게 됩니다. 즉 어떤 두 원소 a 와 b 가 비교되었다는 뜻은 a 와 b 중 둘 중 하나가 피벗이라는 뜻이지요.
편의상 a 가 피벗이라고 해봅시다. 그렇다면, b 는 a 의 왼쪽 혹은 오른쪽에 위치한 배열에 들어가게 되고, 결국 a 와는 영원히 이별하게 되겠지요. 따라서 어떤 두 원소는 최대 1 번 비교할 수 있습니다.
자 이제, 우리가 정렬하고자 하는 원소들을 크기 순으로 $a_1, a_2, \cdots, a_n$ 이라고 합시다. 그리고 다음과 같은 확률 변수 $X_{ij}$ 를 생각해봅시다.
$X_{ij} = \begin{cases} 1 &a_i \text{ 와 } a_j \text{ 가 비교됨} \\ 0 & \text{아닐 경우} \end{cases}$
이는 흔히 Indicator variable 이라 하는데, 어떠한 사건이 발생하면 1 이고, 발생하지 않으면 0 이 되는 확률 변수 입니다. 우리의 궁극적인 목표는 전체 원소 사이의 비교가 몇 번 일어났냐를 알아내는 것이기 때문에, 아래의 기댓값을 계산해야 합니다.
$E[\sum_{i=1}^n \sum_{j = i + 1}^n X_{ij}]$
이를 통해 전체 원소 사이의 비교가 평균적으로 몇 번 발생하였는지 알 수 있겠지요. 위 다 합친 것을 한 번에 계산하는 것은 불가능에 가깝습니다. 하지만 기대값이 선형이라는 점을 이용한다면 위 식을 아래와 같이 바꿀 수 있습니다.
$E[\sum_{i=1}^n \sum_{j = i + 1}^n X_{ij}] = \sum_{i=1}^n \sum_{j = i + 1}^n E[X_{ij}]$
즉 $X_{ij}$ 하나의 기대값이 얼만지 알아낸 뒤에 다 더해주면 끝입니다!
자 이제 문제는 두 원소 $a_i$ 와 $a_j$ 가 비교될 확률이 얼마인지 알아내면 됩니다. 앞서 두 원소가 비교되기 위해서라면 $a_i$ 나 $a_j$ 중 둘 중 하나가 피벗으로 택해지고, 그 때 까지 상대 원소가 같은 파티션 안에 들어 있어야 하겠지요.
그렇다면 다음과 같이 3 가지 경우로 나누어 볼 수 있습니다.
피벗으로 $a_p < a_i, a_j$ 인 것이 택해질 경우 : $a_i, a_j$ 는 같은 파티션에 남아 있게 됩니다.
피벗으로 $a_i, a_j < a_p$ 가 택해질 경우 : 역시 $a_i, a_j$ 는 같은 파티션에 남아 있게 됩니다.
피벗으로 $a_i \le a_p \le a_j$ 가 택해질 경우 : 만일 $a_p$ 가 $a_i$ 거나 $a_j$ 중 하나라면, 비교가 수행됩니다. 하지만 $a_p$ 가 그 사이의 원소라면, $a_i$ 와 $a_j$ 는 각기 다른 파티션에 들어가게 되서 영원히 이별하게 되겠지요.
따라서 중요한 부분은 $a_i \le a_p \le a_j$ 인 $a_p$ 가 택해지는 경우입니다. 그 외에는 다시 $a_i, a_j$ 가 같은 파티션에 들어가게 되서, 또 한번의 기회를 부여 받게 되는 것이지요.
쉽게 생각해서 다트판에 $a_i$ 와 $a_j$ 가 있어서 다트를 던져서 이를 맞추는 것이라 생각하면 됩니다. 그 대신 다트판 밖에 다트을 던지면 (즉 $a_p$ 가 $a_i$ 보다 작거나 $a_j$ 보다 클 경우) 다시 다트를 던질 수 있습니다. 결과적으로, 다트로 $a_i$ 나 $a_j$ 를 맞출 확률은 다트판의 크기 분의 2 가 될 것입니다.
따라서, $a_i$ 와 $a_j$ 를 맞출 확률은 아래와 같이;
$P[X_{ij} = 1] = \frac{2}{j - i + 1}$
로 나타낼 수 있습니다. 분자는 일단 $a_i$ 와 $a_j$ 두 개 이므로 2 가 오고, 분모에는 $a_i$ 와 $a_j$ 사이의 원소의 개수인 $j - i + 1$ 가 오게 되겠죠.
따라서 기대값은
$E[X_{ij}] = 1 \cdot P[X_{ij} = 1] + 0 \cdot P[X_{ij} = 0] = \frac{2}{j - i + 1}$
가 됩니다.
결과적으로 전체 평균 비교 횟수는 아래와 같이 나타내집니다.
$\sum_{i=1}^n \sum_{j = i + 1}^n E[X_{ij} = \sum_{i=1}^n \sum_{j = i + 1}^n \frac{2}{j - i + 1}$
좀 더 정리해보자면
$\sum_{i=1}^n \sum_{j = i + 1}^n \frac{2}{j - i + 1} < \sum_{i=1} 2(1 + \frac{1}{2} + \cdots + \frac{1}{n}) = 2n(1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n})$
가 됩니다. 위와 같이 우변에 있는 역수들의 합은 조화 급수(Harmonic series) 라고 하는데, 아래와 같은 방법으로 근사할 수 있습니다.
$1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} < 1 + \int_1^n \frac{1}{x} dx = 1 + \log n$
결과적으로 우리의 기대값은 아래와 같이 Big-O 로 나타낼 수 있게 됩니다.
$E[\sum_{i=1}^n \sum_{j = i + 1}^n X_{ij}] < 2n(1 + \log n) = \mathcal{O}(n \log n)$
우리의 무작위로 피벗을 택하는 퀵소트의 시간 복잡도는 $\mathcal{O}(n\log n)$ 이 됨을 알 수 있습니다!
그래서 정렬 알고리즘을 뭘 써야 하는데?
대부분의 라이브러리에서 제공되는 sort 함수의 경우 퀵 소트를 기반으로 해서 여러가지 정렬 알고리즘을 혼합해서 사용하고 있습니다. 왜냐하면 어떤 정렬 알고리즘은 원소의 개수가 적을 때 훨씬 빠르고 어떤 알고리즘은 그 수가 클 때 효과를 발휘하기 때문이지요.
예를 들어서 GCC 의 C++ 라이브러리인 libstdc++ 의 경우 sort 함수는 특정 깊이 까지 partition 을 하고, 적당히 파티션의 크기가 작아졌다면 힙소트(Heapsort) 라는 방식의 정렬을 수행합니다. 이 힙 소트는 퀵 소트에 비해 원소의 수가 적을 때 퀵 소트 보다 더 빠릅니다.
또한 한 가지 중요한 것은 이 강좌에서 퀵 소트를 배웠다고 해서 절대로 정렬 함수를 직접 구현해서 쓰면 안됩니다. 실제 프로그래밍 할 때에는 라이브러리에서 제공되는 sort 함수를 사용하는 것이 언제나 옳습니다. 왜냐하면 라이브러리 에서 제공되는 정렬 함수들은 수 많은 벤치 마크를 통해 검증된 것이므로, 여러분이 어떤 방식으로 퀵 소트를 구현하든 라이브러리의 정렬 함수보다는 느릴 것입니다.
자 그럼 이것으로 이번 강좌를 마치도록 하겠습니다. 다음 강좌에서는 조금 다른 방식으로 작동하는 정렬 알고리즘에 대해서 알아보도록 하겠습니다.
생각 해보기
문제 1
앞서 이야기한 여러가지 피벗을 고르는 방식으로 퀵 소트를 구현해보세요.
댓글을 불러오는 중입니다..