모두의 코드
모두의 알고리즘 - 2 - 1. 정렬 알고리즘과 분할 정복
안녕하세요 여러분! 이제 부터 본격적으로 여러가지 알고리즘들에 대해 알아볼 것입니다.
이번 강좌에서는 컴퓨터에서 가장 많이 쓰인다고 볼 수 있는 정렬(sorting) 알고리즘에 대해 알아보겠습니다.
정렬이란, 어떠한 데이터를 순서대로 정리하는 작업을 말합니다. 여기서 데이터는, 수 데이터가 될 수 도 있고, 문자열이 될 수 도 있고, 아니면 심지어 대소 관계가 정의되어 있는 임의의 객체도 될 수 있습니다.
정렬은 거의 모든 곳에서 사용 됩니다. 예컨대 수능을 보신 분들이라면 알겠지만, 성적표에 내 성적이 백분위 몇 % 인지 찍혀 있는 것을 알 수 있습니다. 이를 계산하기 위해서는, 전체 수험생의 성적을 순서대로 정렬한 뒤에, 내 성적이 몇 번째 인지만 안다면 백분위를 쉽게 알 수 있습니다.
혹은 아마존과 같은 온라인 쇼핑몰을 생각해본다면 물건들을 가격 순서대로 볼 수 도 있고, 아니면 평점 순으로도 볼 수 있을 것입니다. 이를 위해서라면, 가격 순으로 혹은 평점 순으로 정렬을 할 수 있어야겠지요.
게다가 정렬은 원하는 데이터를 빠른 속도로 찾을 수 있게 도와줍니다. 예컨대 사전에 있는 단어들이 무작위 순서로 나열되어 있다면 어떨까요? 우리가 원하는 단어를 찾기 위해서라면 사전의 처음 부터 끝까지 훑어 보아야될 것입니다. 이렇게 헛수고를 하지 않아도 되는 이유는 사전에 있는 단어들이 오름차순으로 정렬되어 있기 때문이지요.
실제로 컴퓨터에서도 정렬된 데이터에서의 탐색은 뒤에서 나올 이진 탐색 을 통해 정렬되지 않은 데이터에 비해 훨씬 빠르게 수행할 수 있습니다.
이와 같이 정렬은 수 많은 곳에서 사용되고 있습니다. 많은 컴퓨터 과학자들이 어떻게 하면 정렬을 빠르게 할 수 있을지에 대해 연구를 하였습니다.
그렇다면 어떻게 하면 정렬을 빨리 할 수 있을까요? 일단 가장 단순한 방법으로 어떻게 하면 정렬을 수행할 수 있을지 부터 생각해보도록 합시다.
버블 정렬 (Bubble sort)
기본적인 아이디어는 다음과 같습니다.
가장 큰 원소를 배열 맨 뒤로 보내자!
그렇다면 이 아이디어를 바탕으로 코드를 짜면 바로 아래와 같습니다.
def bubble_sort(data): for i in range(1, len(data)): for j in range(len(data) - i): if data[j] > data[j + 1]: data[j], data[j + 1] = data[j + 1], data[j] return data
#include <iostream> #include <vector> using namespace std; template <typename T> void sort_list(vector<T>& data) { for (size_t i = 1; i < data.size(); i++) { for (size_t j = 0; j < data.size() - i; j++) { if (data[j] > data[j + 1]) { // data[j] 와 data[j + 1] 의 위치를 바꾼다 T temp = std::move(data[j]); data[j] = std::move(data[j + 1]); data[j + 1] = std::move(temp); } } } } int main() { vector<int> s = {1, 9, 8, 5, 4, 6, 7, 3, 2, 10}; sort_list(s); for (int num : s) { cout << num << " "; } }
일단 첫 번째 loop 에서 i 의 값이 1 부터 len(data) - 1 까지 변합니다. 이 때 여기서 i 가 나타내는 값은 뒤에서 부터 몇 번째 원소에 최대값을 가져다 놓으면 되냐를 나타냅니다.
즉 맨 처음에 i 가 1 일 때는 맨 뒤에 최대값 원소를 가져다 놓는다는 의미고, len(data) - 1 일 때에는, 맨 처음에서 두 번째 원소에 최대값 원소를 가져다 놓는다는 의미 입니다.
그리고 j 는 0 부터 최대값 원소를 가져다 놓을 위치 바로 직전까지 움직이면서, 왼쪽의 값이 오른쪽의 값 보다 크면 그 서로의 위치를 바꾸게 됩니다. 예를 들어서 1, 4, 2, 3 이라는 데이터를 정렬 하는 경우;
1, 4, 3, 2 -> 1, 4, 3, 2
1, 4, 3, 2 -> 1, 3, 4, 2
1, 3, 4, 2 -> 1, 3, 2, 4
처음에 위와 같은 과정을 거치게 됩니다. 한 가지 중요한 점은, 전체 배열에서 가장 큰 원소 (4) 가 맨 뒤로 왔다는 점입니다. 이 알고리즘의 이름도 사실 여기서 따온 것인데, 가장 큰 원소가 맨 뒤로 마치 탄산음료의 기포 처럼 위로 올라온다고 해서 거품 정렬 (Bubble sort) 가 되겠습니다.
그 다음 pass 에서는 어차피 맨 뒤에는 가장 큰 원소가 자기 자리에 와있으므로, 앞의 3 개의 원소만 확인하면 됩니다. 그리고 그 3 개의 원소들 중에서 가장 큰 원소인 3 이 맨 뒤에서 두 번째 자리에 오게 되겠지요. 이 과정은 아래와 같습니다.
1, 3, 2, 4 -> 1, 3, 2, 4
1, 3, 2, 4 -> 1, 2, 3, 4
그리고 마지막으로 앞의 두 원소를 확인하며 위 정렬 알고리즘은 끝이 나게 됩니다.
그렇다면 위 알고리즘의 메모리 복잡도는 얼마일까요? 거품 정렬의 경우 원래 데이터가 저장되어 있는 배열을 제외하고는 거의 사용하지 않습니다. (두 원소 swap 을 위한 temp 한 개 만 쓴다고 보도도 됩니다.) 즉 메모리 복잡도는 $\mathcal{O}(1)$ 로 매우 훌륭합니다. 이와 같이 정렬을 위해 메모리를
하지만 거품 정렬의 시간 복잡도는 어떨까요? 위 데이터의 수가 $n$ 이라 할 때 두 개의 for loop 이 각각 $n$ 과 $n - 1$ 번 돌아가므로, 총 $n(n-1) = n^2 - n$ 번의 연산을 수행한다고 볼 수 있습니다. 즉 Big-O 표기법으로 나타내자면, $\mathcal{O}(n^2)$ 이 되겠습니다.
보시다시피 위 알고리즘은 매우 간단합니다. 하지만 지난번 강좌에서 다루었듯이 $\mathcal{O}(n^2)$ 의 시간 복잡도는 그리 바람직하지는 않습니다.
예를 들어서 우리나라 전 국민의 전화번호를 정렬하고 싶다고 합시다. 대충 전화번호의 개수가 5천만개가 있다고 하면, 위 알고리즘은 대충 $(5 \times 10^7)^2 \approx 2 \times 10^{15}$ 번 정도의 연산을 해야 합니다. 통상적으로 일반적인 컴퓨터는 1 초에 $10^9$ 번 정도의 연산을 한다고 보는데, 이를 위해서는 대충 $2 \times 10^6$초, 즉 대충 23 일 정도 걸리네요. 매우 느립니다.
그렇다면 왜 버블 정렬은 느릴까요? 답은 간단합니다. 두 원소를 비교함으로써 얻은 정보를 충분히 사용하고 있지 않기 때문이지요. 쉽게 말해, 굳이 해야되지 않을 비교들을 계속 하고 있다는 점입니다. 예를 들어서,
$a < b, b < c \rightarrow a < c$
위와 같이 $a$ 랑 $b$ 랑 비교했을 때, $a$ 가 더 작고, $b$ 랑 $c$ 와 비교 하였을 때 $b$ 가 더 작다면, 굳이 $a$ 랑 $c$ 를 비교하지 않아도 $a$ 가 더 작을 것이라는 점을 알 수 있습니다. 따라서 실제로 정렬 알고리즘을 잘 설계한다면, 위와 같이 불필요한 비교를 줄일 수 있습니다.
병합 정렬 (Merge sort)
병합 정렬은, 거품 정렬의 느린 속도를 해결하기 위해 만들어진 정렬 알고리즘 입니다. 1945년에 폰 노이만에 의해 개발되었다고 알려져 있습니다.
병합정렬의 기본적인 아이디어는 간단합니다. 만약에 이미 정렬되어 있는 두 개의 데이터들이 있다고 생각해봅시다. 이 들을 어떻게 하면 쉽게 합칠 수 있을까요?
위 경우 배열 A 에는 [2, 5, 7, 10] 이 있고, 배열 B 에는 [1, 3, 8, 9] 가 저장되어 있습니다. 만약에 이 배열이 각각 정렬되어 있다는 사실을 알고 있다면, A 와 B 를 합친 배열([2, 5, 7, 10, 1, 3, 8, 9])을 빠르게 정렬할 수 있게 됩니다.
왜냐고요? 일단 A 와 B 를 합쳤을 때 가장 작은 원소를 어떻게 찾는지 알아봅시다.
A 와 B 가 각각 정렬되어 있기 때문에, A + B 를 하였을 때의 최소 원소는 당연히 A 의 최소 원소거나, B 의 최소 원소가 될 것입니다. 따라서, 단 한 번의 비교 만으로 A + B 에 올 첫 번째 원소를 알아낼 수 있습니다.
만일 A 와 B 가 각각 정렬된 상태가 아니였다면, A + B 의 최소 원소를 알아내기 위해서라면 전체 배열을 순회해야 겠지요. 즉 $\mathcal{O}(n)$ 의 시간이 걸렸을 것입니다. 하지만 A 와 B 가 정렬되어 있었기에 $\mathcal{O}(1)$ 로 찾아낼 수 있습니다!
그렇다면 그 다음으로 작은 원소는 어떻게 찾을까요? 매우 간단합니다. 방금 B 의 원소 1 을 A + B 의 첫 번째 원소로 써 넣었으므로, 이제 B 는 마치 [3, 8, 9] 만 있다고 보면 됩니다. 따라서, 그 다음에 올 원소는 [2, 5, 7, 10] 과 [3, 8, 9] 의 최소 원소 이므로;
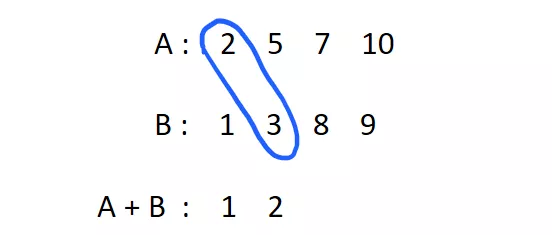
2 가 오겠네요.
따라서 위의 방식 대로 두 개의 정렬된 배열을 하나의 정렬된 배열로 합치는 작업은 각각의 원소 당 $\mathcal{O}(1)$ 로 할 수 있기에, 합친 배열의 원소의 개수가 $n$ 개 라면 총 $\mathcal{O}(n)$ 의 시간 복잡도로 수행 할 수 있습니다. (앞서 버블 정렬의 경우에는 $\mathcal{O}(n^2)$ 였죠)
위 과정을 코드로 나타낸다면 아래와 같습니다.
def merge(A, B): # 두 배열이 비어있지 않는지 확인한다. if len(A) == 0: return B elif len(B) == 0: return A # 현재 A 와 B 의 몇 번째 원소를 확인하는지 나타내는 변수 current_a = 0 current_b = 0 sorted = [] while current_a < len(A) and current_b < len(B): if A[current_a] <= B[current_b]: sorted.append(A[current_a]) current_a += 1 # 만약에 A 의 원소를 모두 추가하였다면, B 의 나머지 # 원소들을 그냥 sorted 에 더해주면 됨. if current_a == len(A): sorted += B[current_b:] return sorted elif A[current_a] > B[current_b]: sorted.append(B[current_b]) current_b += 1 if current_b == len(B): sorted += A[current_a:] return sorted return sorted
#include <iostream> #include <vector> using namespace std; // 두 벡터를 합친 벡터를 반환한다. template <typename T> vector<T> merge(const vector<T>& A, const vector<T>& B) { if (A.empty()) { return B; } else if (B.empty()) { return A; } vector<T> merged; merged.reserve(A.size() + B.size()); size_t current_a = 0, current_b = 0; while (current_a < A.size() && current_b < B.size()) { if (A[current_a] <= B[current_b]) { merged.push_back(A[current_a++]); if (current_a == A.size()) { merged.insert(merged.end(), B.begin() + current_b, B.end()); return merged; } } else if (A[current_a] > B[current_b]) { merged.push_back(B[current_b++]); if (current_b == B.size()) { merged.insert(merged.end(), A.begin() + current_a, A.end()); return merged; } } } return merged; } int main() { vector<int> A = {2, 5, 7, 10}; vector<int> B = {1, 3, 8, 9}; vector<int> merged = merge(A, B); for (int num : merged) { cout << num << " "; } }
자 이제 위에서 정의한 병합(merge) 함수를 통해서 정렬을 수행한다고 생각해봅시다. 이를 이용해서 어떻게 전체 배열의 정렬을 수행할 수 있을까요? 어찌 되었든 병합을 하기 위해서는 정렬된 두 배열을 준비해야 되고, 다시 이 배열들을 준비하기 위해서는 어찌되었든 정렬된 배열을 준비해야 되고...
하지만 영원히 정렬을 못하는 것은 아닙니다. 왜냐하면 크기가 1 인 배열은 이미 정렬된 상태로 간주할 수 있기 때문이지요. 따라서 크기가 2 인 배열을 정렬하기 위해서는 이를 반으로 나누어서 위의 merge 함수를 호출하면 됩니다.
그렇다면 크기가 4 인 배열은 어떨까요? 앞서 크기가 2 인 배열을 정렬할 수 있게 되었으므로, 크기가 4 인 배열을 반으로 나누어서 각각을 정렬하고 이를 merge 하면 됩니다. 결국에는 임의의 크기의 배열도 위 merge 를 사용하면 정렬할 수 있게 됩니다.
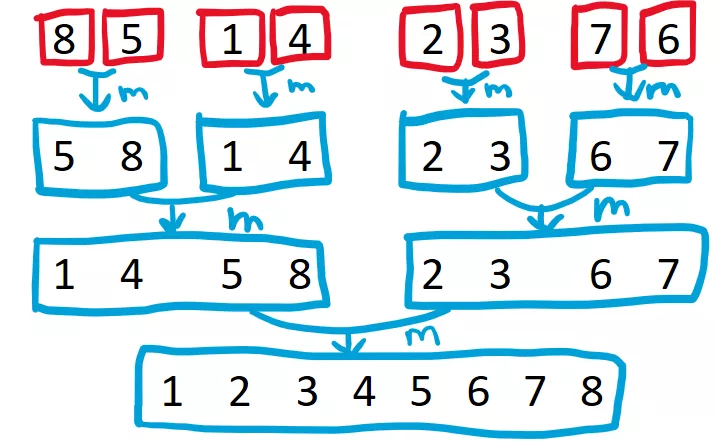
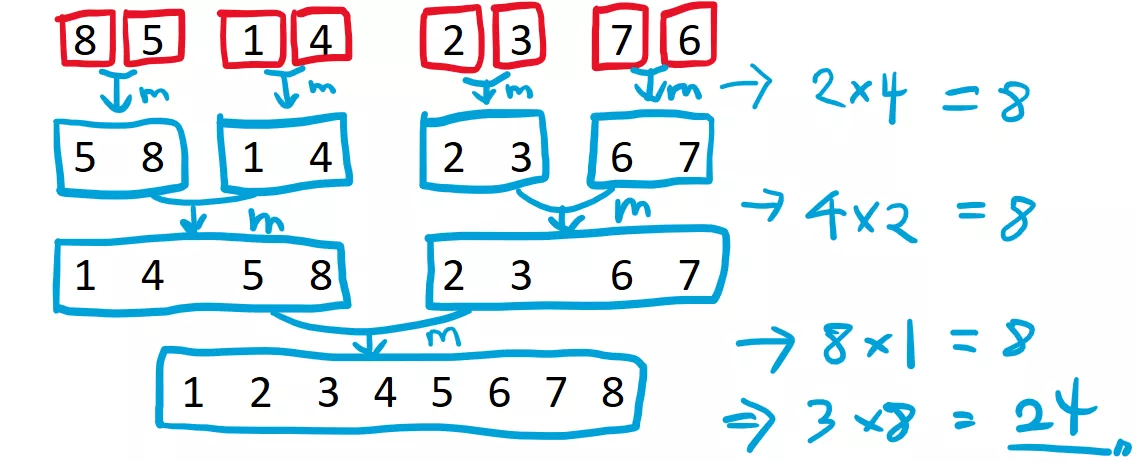
아래 그림으로 이해하면 더 쉽습니다. 예컨대 [8, 5, 1, 4, 2, 3, 7, 6] 을 어떤식으로 정렬하는지 살펴보도록 합시다.
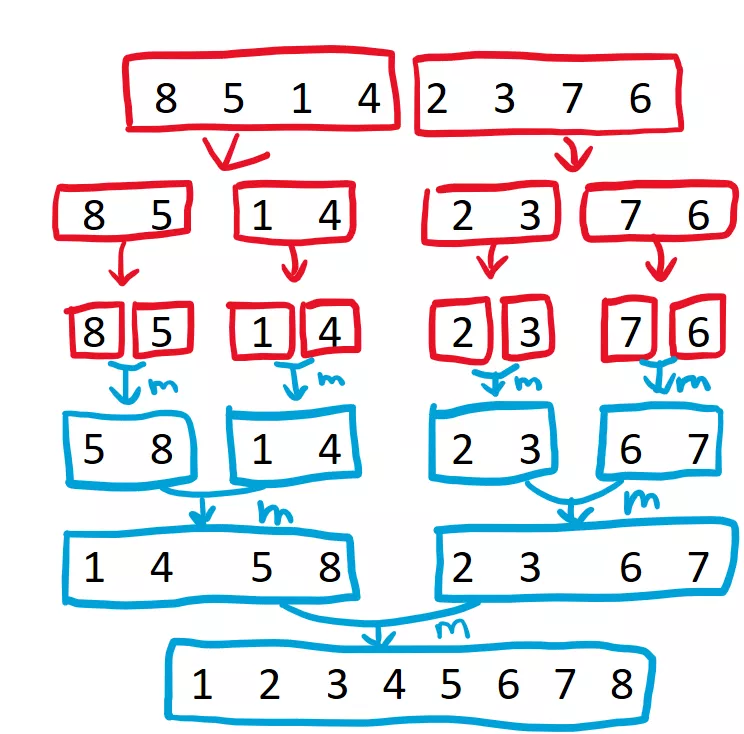
merge 함수를 호출하기 위해서는 이미 정렬된 두 배열을 준비해야 합니다. 따라서, 위 경우 8, 5, 1, 4 와 2, 3, 7, 6 을 어떻게든 정렬을 해야지만 병합을 할 수 있게 됩니다.
마찬가지로 8, 5, 1, 4 를 정렬하기 위해서는 8, 5 와 1, 4 각각을 정렬을 해야지만 병합을 할 수 있게 됩니다.
마지막으로 8, 5 를 정렬하기 위해서는 8 과 5 각각을 정렬해야 하고, 1, 4 를 정렬하기 위해서는 1, 4 각각을 정렬해야 하는데, 원소 한 개 짜리 배열은 이미 정렬된 것으로 간주될 수 있으므로, 무사히 병합을 수행할 수 있게 됩니다.
이 부분이 위 그림에서 파란색으로 m 이라고 써있는 부분 입니다. 이제 5, 8 과 1, 4 로 각각 정렬되어 있으므로, 이를 다시 병합 하면 [8, 5, 1, 4] 의 정렬된 결과인 [1, 4, 5, 8] 을 얻을 수 있습니다. 마찬가지로 [2, 3, 7, 6] 부분 역시 정렬된 배열인 [2, 3, 6, 7] 을 얻을 수 있고, 마지막으로 다시 한 번 더 병합 한다면 [1, 2, 3, 4, 5, 6, 7, 8] 을 얻게 됩니다.
아래 영상을 보신다면 더 쉽게 이해하실 수 있을 것입니다.
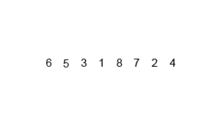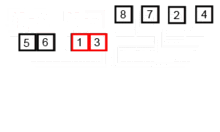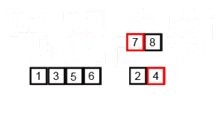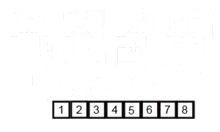
이 과정을 코드로 나타내면 아래와 같습니다.
# 위에서 만든 merge 함수를 사용한다! def merge_sort(data): if len(data) <= 1: return data mid = len(data) // 2 # 왼쪽 부분을 정렬 left = merge_sort(data[:mid]) # 오른쪽 부분을 정렬 right = merge_sort(data[mid:]) # 정렬된 것을 합친다. return merge(left, right)
// 위에서 만든 merge 함수를 사용한다. template <typename T> vector<T> merge_sort(const vector<T>& data) { if (data.size() <= 1) { return data; } size_t mid = data.size() / 2; const auto left = merge_sort(vector<T>(data.begin(), data.begin() + mid)); const auto right = merge_sort(vector<T>(data.begin() + mid, data.end())); return merge(left, right); } int main() { auto merged = merge_sort(vector<int>{8, 5, 1, 4, 2, 3, 7, 6}); for (int num : merged) { cout << num << " "; } }
그렇다면 이 알고리즘이 과연 버블 소트보다 빠를까요? 이 알고리즘의 시간 복잡도는 어떻게 계산할까요? 위 알고리즘에서 연산이 실행되는 부분은 앞서 그림에서 파란색으로 나타낸 merge 함수가 호출되는 부분 입니다.
그리고 앞서 merge 함수의 경우 합쳐진 배열의 크기가 $n$ 이라면, merge 연산이 $\mathcal{O}(n)$ 으로 수행된다는 사실을 알고 있습니다. 따라서, 위 정렬의 경우 각 단계에서 수행되는 연산의 회수는 다음과 같습니다.
위 경우 첫 번째 단계에서 (1 개 짜리 배열 두 개를 2 개 짜리 배열로 합칠 때), 총 $2 \times 4 = 8$ 번의 연산을 수행합니다. 그리고 두 번째 단계에서는 좀 더 큰 배열을 하나로 합치지만, merge 를 하는 횟수 자체는 절반으로 줄어들어서 총 $4 \times 2 = 8$ 번의 연산을 수행하고, 마지막 단계에서는 merge 한 번을 4 개 짜리 원소 배열 두 개를 합치는데 한 번 사용하기 때문에 $8 \times 1= 8$ 번의 연산이 수행됩니다.
따라서 총 24 번의 연산이 수행되었습니다. 이를 일반화 시켜서 크기가 $2^n$ 인 배열을 정렬할 경우 시간 복잡도가 어떻게 될지 생각해봅시다.
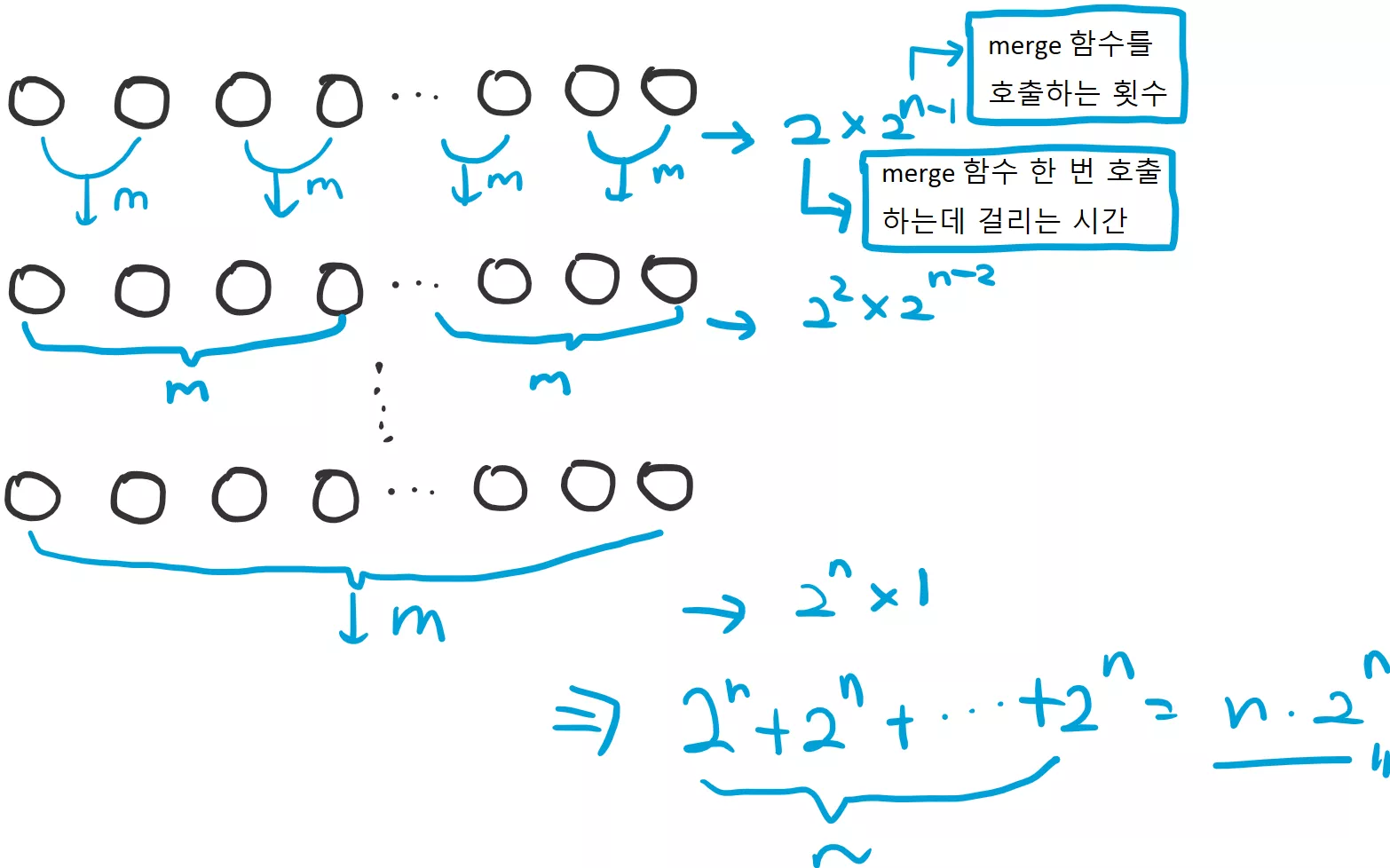
첫 번째 단계에서는 크기가 2 인 배열로 merge 하는 작업을 총 $2^{n-1}$ 번 수행할 것입니다. 그 다음 단계에서는 2 인 배열 두 개를 크기가 $4 = 2^2$ 인 배열로 merge 하는 작업을 총 $2^{n-2}$ 번 하겠지요. 그 다음에는 크기가 $2^3$ 인 배열로 merge 하는 작업을 $2^{n-3}$ 번 하고 맨 마지막에는 크기가 $2^{n-1}$ 인 정렬된 배열 두 개를 merge 하는 작업을 딱 한 번 할 것입니다.
전체 시간 복잡도를 식으로 표현하자면 다음과 같습니다.
$ \mathcal{O}(2) \times 2^{n-1} + \mathcal{O}(2^2) \times 2^{n-2} + \cdots + \mathcal{O}(2^{n-1}) \times 2 + \mathcal{O}(2^n) \times 1 = \mathcal{O}(n \cdot 2^n) $
위는 배열 전체의 원소의 개수가 $2^n$ 개 였을 때의 시간 복잡도를 의미합니다. 따라서 만약에 원소의 개수가 $n$ 개 였다면, $\mathcal{O}(n\log n)$ 번 걸렸을 것입니다. ($2^n$ 이 $n$ 에 대응되고, $n$ 이 $\log n$ 에 대응됨) 참고로 여기서 $log$ 는 밑이 2 인 log 입니다만, 사실 그게 big-O 표기법에서 중요하지는 않습니다. 왜냐하면 어차피 밑이 다른 $log$ 끼리는 상수배 차이나기 때문이죠.
따라서 이 병합 정렬의 전체 시간 복잡도는 $\mathcal{O}(n \log n)$ 이 됩니다. 이는 거품 정렬의 $\mathcal{O}(n^2)$ 보다 훨씬 빠릅니다! 앞서 5천만명의 데이터를 정렬할 때, 병합 정렬을 사용하면 $5 \times 10^7 \times \log (5 \times 10^7) \approx 3.8 \times 10^8$ 의 연산으로도 정렬할 수 있게 됩니다. 이는 대략 0.4 초 면 충분합니다! 버블 소트의 경우 23 일 정도 걸렸데 말이죠.
이것이 바로 좋은 알고리즘을 사용해야 하는 이유 입니다. 작업의 속도를 정말 믿을 수 없을 정도로 단축 시킬 수 있습니다.
분할 정복 (Divide and Conquer)
분할 정복은 알고리즘을 설계하는데 있어서 자주 쓰이는 방식 중 하나 입니다. 이름에도 알 수 있듯이, 원래 풀고자 하는 어려운 문제를, 좀 더 쉽고 작은 문제로 쪼개서 각개 격파를 하는 방식 입니다.
분할 정복 방식의 알고리즘은 다음과 같은 두 가지 단계로 구성됩니다.
문제를 쪼개는 단계
쪼갠 문제를 합치는 단계
병합 정렬의 경우, 원래 풀고자 하는 어려운 문제 (크기 $n$ 의 배열을 정렬하는것) 를 작은 배열들로 쪼개고 (단계 1), merge 를 통해서 쪼갠 문제들을 합쳤습니다 (단계 2).
분할 정복 방식은 정렬 알고리즘에서 흔하게 쓰이는 방식 입니다. 뒤에서 다룰 퀵 소트 (Quick sort) 방식의 정렬도 분할 정복 방식을 사용합니다. 그 외에도 큰 두 수의 곱을 빠르게 계산하기 (Karatsuba algorithm), 평면 상에서 가장 가까운 두 점의 거리 구하기, 빠른 퓨리에 변환 등등 수 없이 많은 알고리즘에서 사용되고 있습니다.
물론 언제나 이 분할 정복 방식이 먹히는 것이 아닙니다. 위 병합 정렬이 빠를 수 있었던 이유는 merge 함수가 매우 빠르게 ($\mathcal{O}(n)$) 으로 수행될 수 있었기 때문이지요.
그렇다면 분할 정복 알고리즘의 시간 복잡도를 쉽게 계산할 수 있는 방법은 없을까요?
마스터 정리 (Master Theorem)
분할 정복과 같이 재귀적으로 표현되는 알고리즘의 시간 복잡도를 쉽게 계산할 수 있도록 도와주는 정리로 마스터 정리 (Master Theorem)가 있습니다.
만약에 어떤 알고리즘이 입력값 $n$ 에 대해서 필요한 연산 횟수를 $T(n)$ 이라고 합시다. 우리의 목표는 이 $T(n)$ 을 적당한 Big-O 표기법으로 나타내는 것입니다.
이 때 $T(n)$ 이 어떠한 상수 $a, b$ 와 어떤 함수 $f(n)$ 에 대해 다음과 같은 관계식을 만족한다고 해봅시다.
$T(n) = aT(\frac{n}{b}) + f(n)$
위와 같은 관계식은 분할 정복을 사용하는 사용하는 알고리즘에서 흔하게 볼 수 있는 형태 입니다. 왜냐하면, $T(\frac{n}{b})$ 부분이 더 작은 문제를 푸는데 걸리는 시간 을 의미하고, $f(n)$ 을 작은 문제 푼 결과를 큰 문제를 풀기 위해 사용하는 과정 이라고 보시면 되기 때문이지요.
위 병합 정렬의 경우
$T(n) = 2T(\frac{n}{2}) + \mathcal{O}(n)$
의 관계식을 만족함을 알 수 있습니다. 왜냐하면, 크기 $n$ 배열을 크기 $n/2$ 인 배열 두 개($=a$)로 쪼개 므로 각각 $T(\frac{n}{2})$ 만큼 걸리게 되고, 이를 합치는 merge 작업이 $\mathcal{O}(n)$ 이 걸리기 때문 입니다.
마스터 정리는 어떤 알고리즘이 위와 같은 관계를 만족할 때 $T$ 이 만족하는 Big-O 를 빠르게 찾을 수 있게 도와줍니다.
편의상 아래와 같은 상수 $c$ 를 정의합시다.
$c = \log_b^a$
이 $c$ 가 나타내는 의미는 다음과 같습니다.
$c = \log_b^a = \frac{\log a}{\log b} = \frac{\log (\text{작은 문제의 개수})}{\log (\text{작은 문제 크기의 역수})}$
즉 문제를 잘게 쪼개면 쪼갤 수 록, 그리고 쪼갠 문제의 크기가 커지면 커질 수 록 $c$ 의 값이 커집니다. $c$ 의 값이 커진다는 것은 더 크고 많은 작은 문제들을 푼다는 의미가 됩니다. 따라서 전체 $T$ 를 줄이기 위해서라면 $f(n)$ 의 연산 횟수가 더 적어져야 되겠지요.
마스터 정리는 다음과 같습니다.
종류 | $f(n)$ 가 만족하는 조건 | $T(n)$ |
|---|---|---|
1 | $f(n) = O(n^{c'})$ 이고 $c' < c$ 일 때 | $T(n) = \mathcal{\Theta}(n^c)$ |
2 | $f(n) = \Theta(n^{c}\log^k n)$ 이고 $k \ge 0$ 일 때 | $T(n) = \mathcal{\Theta}(n^c\log^{k+1}n)$ |
3 | $f(n) = \Omega(n^{c'})$ 이고 $c' > c$ 일 때 | 사실 이 경우는 딱히 $T$ 를 |
예를 들어서 다시 병합 정렬의 관계식을 살펴봅시다.
$T(n) = 2T(\frac{n}{2}) + \mathcal{O}(n)$
이 경우 $a$ 와 $b$ 둘다 2 이므로, $c = \log_2 2 = 1$ 이 됩니다. 그리고, $f(n) = \mathcal{O}(n)$ 이므로, 2 번 경우인 $f(n) = \Theta(n^1 \log^0 n)$ 일 때 임을 알 수 있습니다. (물론 여기서 $f(n)$ 은 Big-O 로 나타내있지만 임의의 f(x) 에 대해 $\Theta(f(x)) \le \mathcal{O}(f(x))$ 이므로 큰 문제가 없습니다.)
따라서 이 경우 $k = 0$ 이므로, $T(n) = \Theta(n^1 \log n) = \Theta(n \log n)$ 이 되어서 우리가 생각했던 결과와 일치합니다.
만약에 병합 정렬의 merge 함수가 $O(n)$ 이 아니라 $O(n^2)$ 이였다면 어떨까요? 이는 위 표에서 3 번 경우에 해당하는데,
$2(\frac{n}{2})^2 = \frac{n^2}{2} < 0.9 n^2$
이 성립하므로 (여기서 $k = 0.9$), $T(n) = \Theta(n^2)$ 이 성립됩니다. 즉, 기존의 버블 정렬과 차이가 없게 됩니다 :(
최대 부분합 문제 (Maximum Subarray problem)
분할 정복으로 풀 수 있는 문제 중 하나로 최대 부분합 문제가 있습니다. 예를 들어서 다음과 같은 상황을 생각해보세요.
철수는 매일 매일 주식을 합니다. 어떤 날은 돈을 잃기도 하고, 어떤 날은 돈을 벌기도 합니다. 이 때, 연속된 날들 중에서 가장 돈을 많이 번 날들의 액수의 합은 얼마일까요?
예를 들어서 철수가 매일 매일
$3, -4, 5, -2, -2, 8, -5, -1, 4$
로 돈을 벌었더라면, 최대 부분 합은 [5, -2, -2, 8] 구간에 해당하는 9 가 될 것입니다.
그렇다면 이 문제를 어떻게 하면 풀 수 있을까요?
일단, 간단히 생각할 수 있는 방법은 그냥 가능한 모든 부분합들 중에서 최대값을 찾는 것입니다. 일단 편의상 $m_i$ 를 $i$ 번째 날 벌거나 잃은 돈의 양이라고 합시다. 그렇다면, 임의의 부분합은 어떤 $i < j$ 에 대해서
$m_i + m_{i + 1} + \cdots + m_j$
가 되겠네요. 만약에 단순히 모든 $i, j$ 쌍에 대해 구한다면 전체 연산의 횟수는
$\sum_{i=1}^n \sum_{j = i}^n (j - i + 1) \approx \mathcal{O}(n^3)$
이 될 것입니다. 왜냐하면 각 부분합을 구하기 위해 $j - i + 1$ 개의 원소들을 더해줘야 되기 때문이지요. 하지만, 살짝 머리를 쓰면 각 부분합을 $\mathcal{O}(1)$ 로도 구할 수 있습니다. 아래와 같은 합을 생각해보세요.
$S_k = \sum_{i = 1}^k m_i$
그렇다면 임의의 부분합은 다음과 같이 단순히 $S_i$ 들 간의 차이로 나타낼 수 있습니다.
$S_{j} - S_{i - 1} = m_i + m_{i + 1} + \cdots + m_j$
따라서 각 부분합을 뺄셈 한 번으로 구할 수 있기 때문에 전체 연산의 횟수는
$\sum_{i=1}^n \sum_{j = i}^n \mathcal{O}(1) \approx \mathcal{O}(n^2)$
로 줄어듭니다. 기존의 $n^3$ 보다는 나쁘지 않지만 $n^2$ 역시 딱히 좋은 것은 아닙니다. 그렇다면 이 문제를 분할 정복에서 얻은 아이디어를 이용해서 어떻게 풀 수 있을지 생각해봅시다.
일단 반으로 나눠보기
무작정 반으로 배열을 반으로 나누어서 각각 처리하는 방식으로 생각해봅시다.
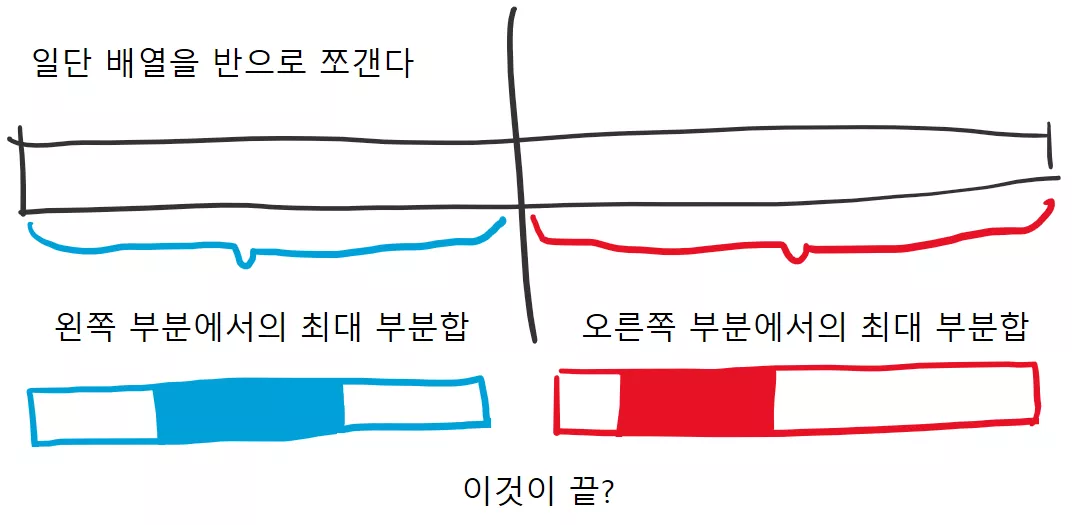
그렇다면 왼쪽 절반에서 최대 부분합 구간(파란색으로 색칠된 부분)을 알아낼 수 있을 것이고, 오른쪽 절반에서 마찬가지로 최대 부분합 구간(빨간색으로 색칠된 부분)을 알아낼 수 있을 것입니다.
그럼 이제 단순히 왼쪽과 오른쪽에서 더 큰 것이 원래 큰 검은색 배열의 최대 부분합 구간이 되는 것일까요? 아닙니다. 아래와 같이 원래 배열에서 최대 부분합 구간이 절반에 걸쳐 있을 수 도 있습니다.
위와 같이 왼쪽과 오른쪽에서만 최대 부분합을 찾게 된다면, 최대 부분합이 가운데 절반을 걸쳐 있는 경우를 빼먹게 됩니다. 따라서, 왼쪽과 오른쪽에서 최대 부분합을 찾은 후에 최대 부분합이 가운데를 지나는 경우 까지 고려 해서 그 중 가장 큰 값을 반환하면 됩니다.
그렇다면, 최대 부분합이 가운데를 지나는 경우를 빠르게 찾을 수 있다면 좋겠지요. 만약에 이 과정이 $\mathcal{O}(n)$ 으로 할 수 있다면, 병합 정렬과 같은 $\mathcal{O}(n\log n)$ 의 속도를 얻을 수 있지만, 그 과정이 $\mathcal{O}(n^2)$ 이라면 원래의 $\mathcal{O}(n^2)$ 로 돌아오겠네요.
하지만 다행이도, 최대 부분합이 가운데를 지나는 경우는 $\mathcal{O}(n)$ 으로 찾을 수 있습니다. 여러분도 생각해보세요.
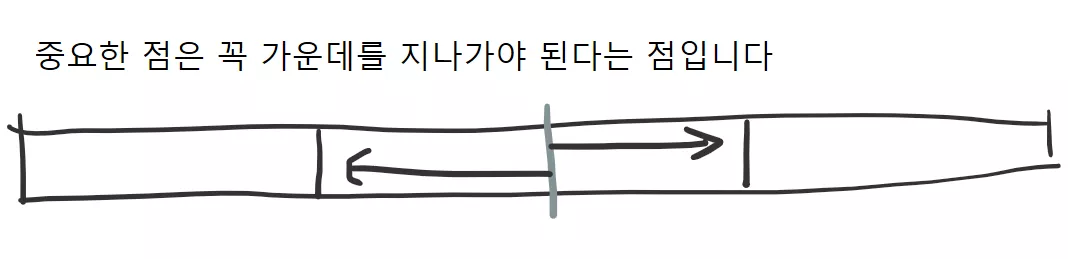
최대 부분합이 가운데를 지나가야 되므로, 가운데에서 시작해서 왼쪽과 오른쪽 방향으로 뻗어나가는 모습으로 생각하시면 됩니다. 가운데를 지나가는 최대 부분합은 왼쪽에서의 최대합과 오른쪽에서의 최대합을 더해주면 되겠지요.
이를 코드로 표현하자면 다음과 같습니다.
# mid 를 지나는 최대 부분합을 반환한다. def max_subarray_cross_mid(data, mid): # 먼저 왼쪽 부분의 최대합을 찾는다. left_max = data[mid - 1] current_sum = data[mid - 1] i = mid - 2 while i >= 0: current_sum += data[i] if current_sum > left_max: left_max = current_sum i -= 1 # 그 다음 오른쪽 부분의 최대합을 찾는다. right_max = data[mid] current_sum = data[mid] i = mid + 1 while i < len(data): current_sum += data[i] if current_sum > right_max: right_max = current_sum i += 1 return left_max + right_max
// mid 를 지나는 최대 부분합을 반환한다. template <typename T> T max_subarray_cross_mid(const vector<T>& data, size_t mid) { T left_max = data[mid - 1]; T current_sum = data[mid - 1]; // (주의) i 의 타입을 size_t 로 하면 0 보다 작은 경우 제대로 확인 못함! int i = mid - 2; while (i >= 0) { current_sum += data[i--]; if (current_sum > left_max) { left_max = current_sum; } } T right_max = data[mid]; current_sum = data[mid]; i = mid + 1; while (i < data.size()) { current_sum += data[i++]; if (current_sum > right_max) { right_max = current_sum; } } return left_max + right_max; }
참고로 주의할 사항은 size_t 는 unsigned int 타입 이기 때문에 0 보다 작은 값은 표현할 수 없습니다. 따라서, i 를 size_t 타입으로 하게 된다면 거꾸로 가는 while 문 (위 경우 while (i >= 0))에서 절대로 빠져나갈 수 없게 됩니다.
그렇다면 이를 바탕으로 전체 알고리즘을 완성하도록 하겠습니다.
def max_subarray(data): if len(data) == 1: if data[0] > 0: return data[0] else: return 0 elif len(data) == 0: return 0 mid = len(data) // 2 # 왼쪽 부분에서의 최대 부분합 left_max = max_subarray(data[:mid]) # 오른쪽 부분에서의 최대 부분합 right_max = max_subarray(data[mid:]) middle_max = max_subarray_cross_mid(data, mid) return max(left_max, right_max, middle_max)
template <typename T> T max_subarray(const vector<T>& data) { if (data.size() == 1) { if (data[0] > 0) { return data[0]; } else { return 0; } } else if (data.size() == 0) { return 0; } size_t mid = data.size() / 2; T left_max = max_subarray(vector<T>(data.begin(), data.begin() + mid)); T right_max = max_subarray(vector<T>(data.begin() + mid, data.end())); T mid_max = max_subarray_cross_mid(data, mid); return max(max(left_max, right_max), mid_max); } int main() { cout << max_subarray(vector<int>{3, -4, 5, -2, -2, 8, -5, -1, 4}); }
위와 같이 분할 정복 방식을 이용해서 최대 부분합 문제를 풀 수 있었습니다.
분할 정복 기법은 알고리즘을 설계 하는데 있어서 매우 많이 등장하는 방식입니다. 어떠한 어려운 문제를 풀기 전에, 이를 작은 문제로 쪼개어서 일단 풀어보고, 이를 바탕으로 큰 문제를 쉽게 풀 수 있다면 분할 정복 방식을 통해 알고리즘의 시간 복잡도를 획기적으로 단축시킬 수 있습니다.
그렇다면 이것으로 이번 강좌를 마치도록 하겠습니다. 다음 강좌에서는 정렬 알고리즘에서 가장 많이 쓰이는 방식인 퀵 정렬(Quick sort) 에 대해 알아보도록 하겠습니다.
생각 해보기
문제 1
우리가 앞서 위에서 구현한 병합 정렬 방식은 불필요한 복사를 많이 수행하고 있습니다. 매 번 배열을 새로 복사해서 전달하기 보다는, 전체 배열은 유지하되 배열의 인덱스들로 부분 배열을 전달한다면 불필요한 복사를 줄일 수 있겠지요. 여러분이 한 번 구현해보시기 바랍니다 (난이도 : 중)
문제 2
병합 정렬의 장점으로 임의 접근(Random Access)가 없고 순차적 접근(Sequential Access) 만 가능한 자료구조에서도 빠르게 정렬을 할 수 있습니다.
임의 접근 이라 하면 어떤 i 번째 원소를 data[i] 와 같이 바로 읽을 수 있다는 뜻입니다. 반면에 순차적 접근은 앞에서 부터 차례대로 읽는 것 밖에 하지 못합니다.
임의 접근이 가능한 자료 구조의 예로는 앞서 우리가 사용한 vector 가 있고, 순차적 접근만 가능한 자료구조는 list 가 되겠지요. 또 다른 예로는 컴퓨터 메모리의 경우 임의 접근과 순차적 접근의 속도가 비슷하지만, 하드 디스크의 경우 순차적 접근이 임의 접근보다 훨씬 빠릅니다.
그렇다면 list 에서 병합 정렬을 구현해보세요! (난이도 : 중)
문제 3
위에서 최대 부분합 문제를 $\mathcal{O}(n \log n)$ 로 해결하였지만 사실은 $\mathcal{O}(n)$ 으로도 해결할 수 있습니다! 한 번 도전해보세요 (참고로 분할 정복 방식은 사용하지 않습니다.)
Hint : i 번째 원소에서 끝나는 최대 부분합을 $S_i$ 라고 합시다. 그렇다면 $S_{i+1}$ 과 $S_i$ 의 관계를 찾을 수 있으신가요? (난이도 : 중)
댓글을 불러오는 중입니다..