모두의 코드
모두의 알고리즘 강좌 시작하기
안녕하세요 여러분. 모두의 알고리즘 강좌에 오신 것을 환영합니다. 언젠가 컴퓨터 알고리즘에 대한 강좌를 꼭 쓰고 싶었는데, 이제 시간이 조금 나서 쓸 수 있을 것 같습니다.
처음에 강의의 이름을 지을 때, 씹어먹는 C 언어 처럼 라임을 맞추고 싶어서 알아먹는 알고리즘으로 할까 고민 하다가, 좀 아닌 것 같아서 택한 이름이 모두의 알고리즘 입니다.
왜 모두의 알고리즘이라 이름을 지었냐면, 사실 블로그 이름이 모두의 코드이기 때문에 이에 맞춰서 이름을 지으려는 의도도 있었지만, 무엇보다도 모든 프로그래머가 기본적으로 알았으면 하는 알고리즘들을 다루고 싶었기 때문입니다.
이 강좌에서는 그 어떤 직군에서 일하는 개발자라도, 즉 서버 개발자든, 게임 개발자든, 아니면 프론트엔트 개발자든 그 어떤 분들이라도 꼭 알았으면 하는 중요한 알고리즘들을 다룰 것입니다.
알고리즘을 왜 배우는가?
알고리즘(Algorithm) 이란, 어떤 문제를 해결하는 방식이란 뜻입니다.

알고리즘이라는 단어 자체는 서기 800년 쯤에 아랍 지역에서 활동하셨던 무하마드 알콰라즈미 라는 사람의 이름에서 따온 것으로, 수학의 여러 분야 (특히 대수학)에 큰 공헌을 하였습니다.
사람의 경우 어떠한 문제를 해결하는 방식을 생각한 다음이 끝이 아니라, 이 방식을 어떻게 실행할 지도 중요합니다. 하지만 컴퓨터의 경우 사용자가 이건 이러한 방식으로 해결해 라고 알려주기만 하면, 컴퓨터가 알아서 그 방식을 따라서 실행하므로, 우리가 올바른 알고리즘만 제시해준다면, 그 이후는 컴퓨터에게 맡기면 됩니다.
이 때문에, 프로그래밍에 있어선 올바른 알고리즘을 제공 하는 것은 매우 중요합니다. 왜냐하면, 사람의 경우, 이리 저리 해보다가 뭔가 이상하다면 융통성 있게 수정하겠지만, 컴퓨터는 정말 우리가 지시한 그대로 따라가기 때문에 처음에 제대로된 알고리즘을 제공해야 합니다. 그 대신 제대로된 알고리즘을 제공해주기만 한다면, 정말 빠르게 처리하겠지요. 물론, 제대로 된 알고리즘에 한해서요.
여러가지 흥미로운 알고리즘들이 사용되는 경우는 매우 많습니다. 예를 들어서 네이버 지도의 길찾기 기능을 생각해보세요.
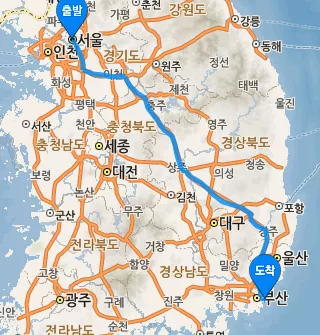
서울에서 부산까지 가능 방법은 무수히 많을 것입니다. 하지만 네이버 지도를 사용해보신 분들은 알겠지만, 그 무수히 많은 경로 중에서도 (일단 경로 자체를 찾는 것도 어렵지만) 가장 최단 시간으로 갈 수 있는 경로를 단 몇 초 안에 계산해서 보여줍니다. 이것이 도대체 어떻게 가능한 것일까요? 이에 대한 해답은 후에 그래프 알고리즘에서 최단 경로 알고리즘을 배울 때 나옵니다.
또다른 예시로 인간의 염색체에서 돌연변이를 찾는 작업을 생각할 수 있습니다. 인간의 염색체는 쉽게 생각해보면 A,T,G,C 이 4 개의 문자로 이루어진 거대한 문자열이라 보시면 됩니다.

보통 인간의 경우 한 개의 염색체에는 5천만개에서 3억개 정도에 달하는 염기쌍이 있다고 보시면 됩니다. 쉽게 말하면, A,T,G,C 로 이루어진 길이가 3억인 문자열 이란 뜻입니다. 이러한 거대한 문자열에서 단순한 방법으로는 우리가 원하는 염기 서열을 찾는다는 것은 거의 불가능에 가깝습니다.
하지만, 후에 강좌에서 배울 문자열 알고리즘을 이용한다면, 단 몇 초 안에 원하는 문자열을 검색할 수 있습니다. 이것이 바로 알고리즘의 힘입니다.
이 강좌에서는 기존에 여러 잘 알려진 문제(정렬, 탐색, 최단 경로 찾기 등등)들에 대해 여러 가지 유명한 알고리즘들에 대해 다룰 것입니다. 또한 더 나아가서, 이러한 알고리즘을 설계하는 알고리즘의 몇 가지 중요한 패러다임들 (동적 계획법(Dynamic programming) 이나 탐욕 알고리즘(Greedy), 분할 정복(Divide and conquer) 같은..)에 대해서 다루어서, 처음 보는 문제라도 어떠한 방식으로 해결하면 될 수 있을 지 감을 잡게 해주는 것이 목표입니다.
또한 무엇보다도, 단순히 알고리즘을 다룰 뿐만이 아니라 이를 실제로 어떻게 구현할지에 대해서도 자세히 다루도록 하겠습니다. 일단 메인은 C++ 로 구현할 텐데, 시간이 난다면 파이썬으로도 어떻게 구현할 것인지에 대해 살펴볼 것입니다.
참고로 이 강좌에서는 데이터를 효율적으로 보관하는 방식인 자료 구조(Data structure)에 대해서는 자세히 다루도록 하지는 않을 것입니다. 자료 구조에 대해서는 같이 연재될 잡아먹는 자료 구조 강좌를 참조하시길 바랍니다.
강의 목차
참고로 강의 계획은 언제든지 바뀔 수 있습니다.
1. 어떤 알고리즘이 효율적인가?
알고리즘의 빠르기를 표현하는 Big-O 표기법 () 에 대해서 다룹니다.
2 - 1. 정렬 알고리즘과 분할 정복
가장 간단한 정렬 알고리즘인 버블 소트(Bubble sort) 부터 시작해서, 가장 많이 쓰이는 보편적인 알고리즘인 병합 정렬(Merge sort) 을 통해 알고리즘 설계 방식 중 하나인 분할 정복(Divide and Conquer)에 대해 다룹니다.
2 - 2. 정렬 알고리즘의 꽃 - 퀵 소트
정렬 알고리즘에서 가장 보적적으로 사용되는 퀵 소트(QuickSort) 알고리즘에 대해 다룹니다.
2 - 3. 비교 기반 정렬 알고리즘의 한계와 여러 가지 다양한 정렬 알고리즘들
비교 기반 정렬 알고리즘의 한계와 함께, 여러가지 다른 형태의 정렬 알고리즘들 (Radix sort 등등) 을 다룹니다.
2 - 4. k 번째 원소를 찾는 알고리즘 - QuickSelect
분할 정복을 사용한 대표적인 알고리즘인 QuickSelect 와 Median of medians 에 대해 다룹니다.
3. 이진 탐색 (Binary search)
정렬된 데이터에서 원하는 내용을 빠르게 찾게 해주는 이진 탐색 알고리즘에 대해 다룹니다.
4 - 1. 그래프 순회 알고리즘 (깊이 우선 탐색과 너비 우선 탐색)
그래프를 순회하는데 많이 사용되는 깊이 우선 탐색 (Depth-First Search) 와 너비 우선 탐색 (Breadth-First Search) 에 대해 다룹니다.
4 - 2. 그래프 최단 경로 알고리즘 1 부 (다익스트라, A*알고리즘)
4 - 3. 그래프 최단 경로 알고리즘 2 부 (벨만 포드 알고리즘, 플로이드 알고리즘)
4 - 4. 그래프 최소 신장 트리 (Minimum spanning tree)
4 - 5. 그래프의 위상 정렬 (Topological sort)
4 - 6. 그래프의 사이클 찾는 알고리즘
4 - 7. 그래프 Max Cut 알고리즘과 그리디(Greedy) 알고리즘
4 - 8. 네트워크 유량 문제 (Max-flow)
5 - 1. 문자열 검색 하기 1 부 (Boyer-Moore)
5 - 2. 문자열 검색 하기 2 부 (Knuth-Morris-Pratt)
5 - 3. 문자열 검색 하기 3 부 (Rabin-Karp)
5 - 4. Longest Common Subsequence 와 Dynamic Programming
최대 공통 문자열(Longest Common Subsequence) 의 문제를 토대로 동적 계획법 방식에 대해 알아봅니다. 비슷한 방법으로 최대 증가 부분 수열 (Longest Increasing Subsequence) 문제도 해결합니다.
5 - 5. 문자열 사이의 Edit distance
6 - 1. 정수를 다루는 알고리즘 (빠른 곱셈, 최대공약수 찾기, 소수 판별, 큰 수의 지수승 등등)
6 - 2. 수치 해석 알고리즘 (방정식의 근 찾기)
7 - 1. 확률적 알고리즘 1 부 - Graph Min-cut
7 - 2. 확률적 알고리즘 2 부 - Median 빠르게 찾기
7 - 3. 확률적 알고리즘 3 부 - 소수 빠르게 판별하기
7 - 4. 확률적 알고리즘 4 부 - 차원 줄이기 (Johnson-Lindenstrauss)
7 - 5. 확률적 알고리즘 5 부 - k SAT 문제
8. Minmax 알고리즘과 Alpha-Beta Pruning

댓글을 불러오는 중입니다..