안녕하세요 여러분! 지난 강좌에서 퀵 정렬 방식은 이해가 잘 되셨나요? 퀵 정렬은 대부분의 라이브러리에서 정렬 함수를 구현할 때 사용하는 가장 보편적인 방식입니다. 물론, 원소의 개수가 작을 때에는 다른 방식으로 정렬하기 하지만, 충분히 클 때에는 퀵 정렬 만큼 빠른 것이 없습니다.

퀵 정렬은 $\mathcal{O}(n \log n)$ 의 시간 복잡도를 자랑합니다. 그런데, 대부분의 정렬 알고리즘들이 퀵 정렬 방식을 사용한다는 뜻은 이것보다 더 나은 방식이 없다는 의미기도 합니다.

그렇다면 정말로 정렬 알고리즘의 시간 복잡도를 $\mathcal{O}(n \log n)$ 보다 빠르게 할 수는 없는 것일까요?

비교 기반 정렬 알고리즘의 한계

퀵 소트와 같은 정렬 알고리즘을 비교 기반 정렬 알고리즘 이라고 부릅니다. 비교 기반이란, 어떤 두 원소의 상대적 순서를 정할 때, 두 원소의 크기를 비교해서 정하기 때문이지요. 그런데 놀랍게도, 모든 비교 기반 정렬 알고리즘은 최소 $\mathcal{O}(n \log n)$ 으로 실행되는 것이 알려져 있습니다.

즉 아무리 머리를 굴려서 비교 기반 정렬 알고리즘을 만들어 봤자 $\mathcal{O}(n \log n)$ 의 벽을 넘을 수는 없다는 것이지요. 이것이 왜 사실인지는 아래에서 알아보도록 합시다.

정렬 이란 것이 과연 무엇인가?

정렬이라는 작업이 무엇인지 엄밀하게 생각해봅시다. 정렬이란,

$a_1, a_2, \cdots, a_n$

과 같은 데이터들이 있을 때, 각각의 $a_i$ 에 번호 $c_i$ 를 할당하는 작업입니다. 이 때 번호들은 $\{ c_1, c_2, \cdots, c_n \} = \{1,2,3,\cdots, n\}$ 이며,

$c_i < c_j \leftrightarrow a_i < a_j $

와 같은 관계가 성립해야 하지요. 쉽게 말해서 예를 들어서 $10, -5, 8$ 과 같은 데이터들이 있다면, 해당 데이터의 $c_i$ 는 각각 $3, 1, 2$ 가 되겠네요. 왜냐하면 정렬을 했을 때 $-5$ 가 맨 앞에 오고 그 다음에 $8$, 그리고 $10$ 이 오게 때문이지요.

결과적으로 정렬 문제는 각 데이터 $a_i$ 에 어떤 순서를 줄지 결정하는 문제와 같습니다.

그런데 문제는 $c_1, \cdots, c_n$ 의 경우의 수가 $n!$ 이라는 점입니다. 그리고, 모든 원소들이 다르다면, 정렬된 상태에서 $c_1, \cdots, c_n$ 들이 가질 수 있는 값은 단 한개 입니다.

따라서 정렬 문제는 이 $n!$ 의 경우의 수 중에서 단 하나의 $c_1, \cdots, c_n$ 을 찾는 문제와 같습니다.

만약에 $a_i$ 와 $a_j$ 를 비교했을 때 그 결과값에 따라 $a_i$ 가 크다면 가능한 $c_1, \cdots, c_n$ 들이 있을 것이고 (이들을 편의상 집합 $C_{a_i > a_j}$ 라 합시다), $a_j$ 가 크다면 가능한 $c_1, \cdots c_n$ 들이 있을 것입니다 (이들은 $C_{a_i < a_j}$).

운이 좋다면 $C_{a_i > a_j}$ 의 크기가 1 이고 $C_{a_i < a_j}$ 의 크기가 $n! - 1$ 인데, $a_i > a_j$ 여서 단 한번의 비교 만으로 $c_1, c_2, \cdots, c_n$ 을 알아 낼 수도 있습니다.

하지만, 그 외의 경우에는 $C_{a_i < a_j}$ 인데, $n! - 1$ 이나 되는 가능성이 남아 있기에 별로 도움이 되지 않습니다. 한 번의 비교로 가능한 모든 경우에 수에서 겨우 1 개만 제외한 셈이 되는 것이니까요.

가장 이상적인 상황은 두 집합의 크기가 동일해서 어느 경우에든 최대한 많은 경우의 수를 날려버리는 것입니다. 즉, $|C_{a_i > a_j}| = |C_{a_i < a_j}| = \frac{n!}{2}$ 가 되는 셈이지요.

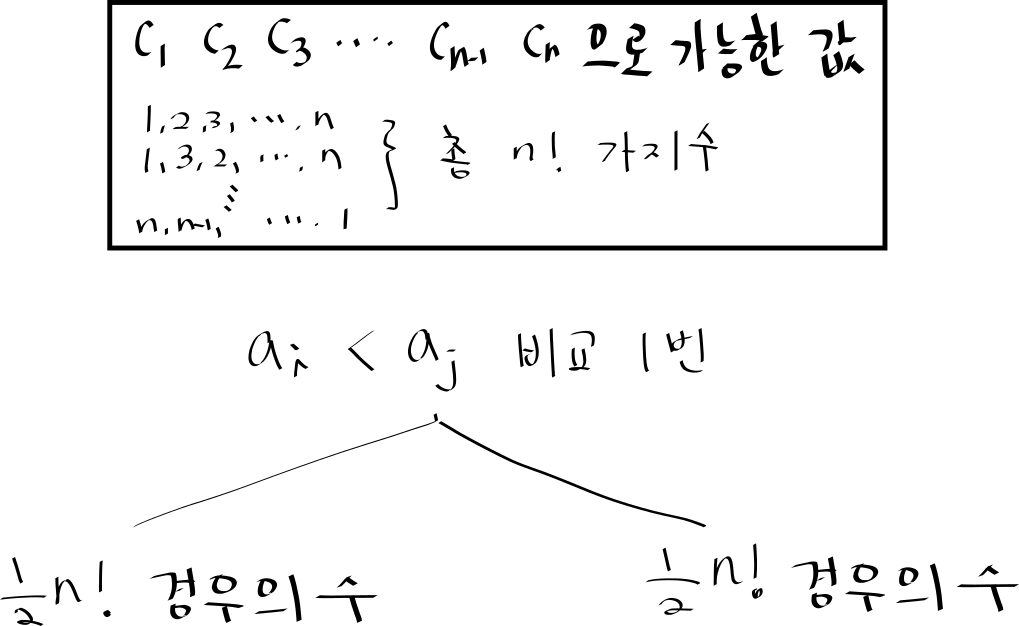
그렇다면 남은 $\frac{n!}{2}$ 의 경우에 수에서 비교를 한 번 더 수행하였을 때 최선의 경우에는 $\frac{n!}{4}$ 개 짜리 집합을 택하게 되겠습니다.

정리하자면 $k$ 번 비교했을 때 만들어지는 $c_1, \cdots, c_n$ 의 경우의 수는 최선의 경우

$\frac{n!}{2^k}$

가 될 것입니다. 그렇다면, 비교를 언제까지 해야 할까요? $c_1, \cdots, c_n$ 을 하나로 정하기 위해서는 당연히 그 경우의 수가 1 이 될때까지 해야 될 것입니다. 따라서

$\frac{n!}{2^k} \le 1$

일 때 까지 수행해야 하겠지요. 따라서 $k$ 는 최소

$\log n! \le k$

와 같은 관계를 만족합니다. 재미있게도 $\log n!$ 은 아래와 같이 근사할 수 있습니다. 일단

$\log n! = \log 1 + \log 2 + \cdots + \log n$

입니다. 로그 그래프를 그려보면

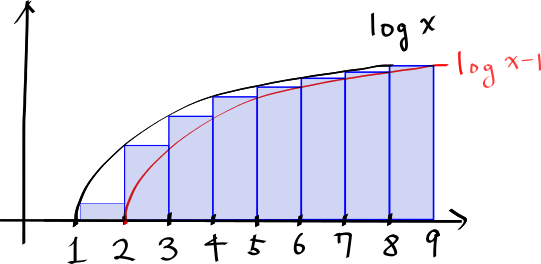
와 같이 나옵니다. 아래의 파란색 기둥들의 넓이의 합은 $\log 1 + \log 2 + \cdots + \log n$ 를 의미합니다. 그리고 그림에서 나타나다시피, 해당 넓이는 $\log x $ 의 아래 넓이보다 작지요.

따라서 우리는 다음과 같은 관계식을 얻을 수 있습니다.

$\int_{1}^{n-1} \log x dx < \log 1 + \log 2 + \cdots + \log n < \int_{1}^{n} \log x dx $

그리고 로그를 적분하면;

$x\log x - x \biggr\rvert_{1}^{n-1} = (n-1)\log (n-1) -n + 2$

따라서;

$\log n! = \mathcal{O}(n\log n)$

임을 알 수 있습니다. 참고로 이와 같은 근사 방법을 스털링 근사(Stirling's approxmiation) 라고 하며 여기에서 좀더 자세한 설명을 볼 수 있습니다.

결론적으로 최소 비교 횟수는 $\mathcal{O}(n\log n)$ 가 됨을 알 수 있습니다.

참으로 안타까운 일이 아닐 수 있습니다. 아무리 노력해도 $\mathcal{O}(n\log n)$ 의 벽을 깰 수 없다니요. 하지만, 여기서 중요한 점은 해당 조건은 비교 기반 알고리즘에 한해서 라는 점입니다. 만약에 비교를 사용하지 않는 정렬 방식이 있다면 더 빠른 정렬 알고리즘을 만들 수 있을 것입니다.

계수 정렬 (Counting Sort)

예를 들어서 여러분이 정수 데이터를 정렬한다고 해봅시다. 예를 들어서 3, 6, 9, 2, 6, 7, 3, 5 와 같은 데이터가 있을 때 여러분은 어떤 방식으로 정렬을 하시나요?

저런 데이터를 퀵 정렬로 정렬하시는 분들도 있나요? 아닙니다. 대충 보아도 2 가 맨앞에 올 것이고, 그 다음에 3, 3, 5, 6, 6, ... 9 순으로 정렬하실 것입니다. 그 이유는 두 가지가 있는데;

• 데이터의 범위가 작고 (최대 9)

• 정수값 자체가 정렬했을 때 그 위치를 대략 알려주기 때문

이죠. 예를 들어서 2 를 보면, 그 크기 자체가 정렬했을 때 대충 두 번째 쯤에 오겠구나 하는 의미를 전달하기 때문입니다.

그렇다면, 최대값 크기의 정수 배열을 만들어서, 각 원소가 몇 번 등장하는지 세면 어떨까요? 예를 들어서 2 는 1번 등장하고, 3 은 2 번 등장하고 하는 식으로 말입니다.

0	1	2	3	4	5	6	7	8	9
0	0	1	2	0	1	2	1	0	1

그 결과는 위 표와 같을 것입니다. 그렇다면 정렬 후에 각 원소들이 어느 위치에 올지 짐작이 가시나요? 예를 들어서 5 의 경우, 자신의 앞에 2 와 3 이 각각 1, 2 개 씩 있으므로, 정렬 후에는 4 번째에 위치하겠지요.

즉, 정렬된 배열에서 각 원소가 첫 번째로 나타나는 위치는 [자신의 앞에 있는 원소들의 개수의 합] 이 되고, 자신이 가장 마지막으로 등장하는 위치는 [자신을 포함한 모든 원소들의 개수의 합 - 1] 이 될 것입니다. 식으로 표현하자면 아래와 같습니다.

원소 $i$ 가 등장하는 횟수가 $c_i$ 라고 한다면 정렬된 배열에서 원소 $i$ 의 위치는 $c_1 + c_2 + \cdots + c_{i - 1} + 1$ 부터 $c_1 + c_2 + \cdots + c_i$ 가 될 것입니다.

만약에 표 앞에서 부터 $c_i$ 를 아래 표 처럼 더해나간다면 어떨까요?

위 처럼 처음에는 $c_0$, 그 다음에는 $c_0 + c_1$, 그 다음에는 $c_0 + c_1 + c_2$ 순으로 해서, $i$ 번째에는 $c_1 + \cdots + c_i$ 가 들어가게됩니다.

아래는 해당 과정을 통해 완성된 표의 모습입니다.

0	1	2	3	4	5	6	7	8	9
0	0	1	2	0	1	2	1	0	1
0	0	1	3	3	4	6	7	7	8

예를 들어서 원소 6 의 경우 해당 합이 6 이므로, 자신이 정렬된 배열에서 가장 마지막으로 등장하는 위치가 6 번째 임을 알 수 있습니다.

따라서 이를 구현하는 아이디어는 간단합니다.

• 먼저 각 원소들의 개수를 세는 배열을 하나 만듭니다. 이는 맨 위의 표와 같습니다.

• 그 다음, 앞에서 부터 원소들을 쭈르륵 더하는 배열을 만듭니다. 이를 편의상 table 이라 부릅시다. (위의 표에서 마지막 열과 같겠네요)

• 원래의 정렬되지 않은 원소들을 쭈르륵 스캔하면서 새로운 정렬된 배열의 적절한 위치에 집어 넣습니다. 예를 들어서 6 의 경우 정렬된 배열의 6 번째와 5 번째 원소로 들어갈 것입니다. 5 의 경우 4 번째 원소로 들어가겠네요.

이를 파이썬과 C++ 로 구현하면 아래와 같습니다.

data = [3, 6, 9, 2, 6, 7, 3, 5]

# 전체 데이터 개수
n = len(data)

# 최대값을 찾는다.
k = max(data)

# 배열을 생성한다.
table = [0] * (k + 1)

# 각 원소가 등장하는 횟수를 구한다.
for element in data:
    table[element] += 1

# 해당 원소가 마지막으로 등장하는 위치를 구한다.
for i in range(1, len(table)):
    table[i] += table[i - 1]

sorted_array = [0] * n

# 왜 거꾸로 참조할까요?
for elem in reversed(data):
    # elem 의 위치는?
    sorted_array[table[elem] - 1] = elem

    # 왜 1 을 빼줄까요?
    table[elem] -= 1

print (sorted_array)

#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;

vector<int> count_sort(const vector<int>& data) {
  int k = *max_element(data.begin(), data.end());
  vector<int> table(k + 1, 0);

  for (int e : data) {
    table[e]++;
  }

  for (int i = 1; i <= k; i++) {
    table[i] += table[i - 1];
  }

  vector<int> sorted(data.size());
  for (auto itr = data.rbegin(); itr != data.rend(); ++itr) {
    sorted[--table[*itr]] = *itr;
  }

  return sorted;
}

template <typename T>
void print(const vector<T>& v) {
  for (const auto& e : v) {
    cout << e << " ";
  }
  cout << endl;
}

int main() {
  vector<int> data = {3, 6, 9, 2, 6, 7, 3, 5};
  cout << "정렬 전 ---------" << endl;
  print(data);

  auto sorted_arr = count_sort(data);
  cout << "정렬 후 ---------" << endl;
  print(sorted_arr);
}

실행 결과

정렬 전 ---------
3 6 9 2 6 7 3 5 
정렬 후 ---------
2 3 3 5 6 6 7 9 

구현 방식에서 주목할 부분이 한 가지 있습니다.

마지막에 data 를 순회할 때 뒤에서 부터 순회한다는 점입니다. 그 이유는 원소들 간의 상대적 순서를 유지하기 위해서입니다.

sorted 배열에 정렬된 원소의 위치를 집어넣을 때 해당 원소가 마지막으로 등장하는 위치 부터 넣습니다. 그 다음으로 같은 원소가 또 등장하였을 때에는 한 칸 왼쪽에 원소를 쓰겠지요. (table[elem] 을 1 감소 시키잖아요.)

따라서, 원래 data 에서 같은 원소라도 상대적으로 왼쪽에 있던 원소는 정렬된 데이터에서도 왼쪽에 나타나게 됩니다.

물론 여기에서는 같은 수 이니까 어차피 구분도 안되는데 굳이 순서를 구분해야 하나라고 물을 수 있는데, 밑에서 기수 정렬 시에 원소들 간에 순서를 유지하는 것이 매우 중요해지므로 일단 참고 넘어가도록 합시다.

계수 정렬의 시간 복잡도

그렇다면 이 계수 정렬의 시간 복잡도는 얼마나 될까요?

먼저 각 원소의 개수를 나타내는 표를 만드는데 시간이 얼마나 걸리는지 살펴보겠습니다. 표를 만들기 위해서는 일단 최대값 부터 찾아야 하겠죠. 최대값은 전체 원소들을 쭈르륵 스캔만 하면 되니까 $\mathcal{O}(n)$ 으로 찾을 수 있습니다. 편의상 최대값을 $k$ 라고 해봅시다.

그 다음 크기가 $k$ 인 표를 만들어서 앞서 본 각 원소들의 개수를 세는 배열을 만들어야 합니다. 이 역시 전체 원소를 한 번만 스캔하면 되므로 $\mathcal{O}(n)$ 면 충분 합니다.

그리고 앞에서부터 개수의 합을 쭈르륵 구해야 합니다. 이 역시 배열을 한 번만 순회하면 되므로 $\mathcal{O}(k)$ 으로 수행할 수 있습니다. ($n$ 이 아니라 $k$ 임에 주목)

마지막으로 sorted 배열에 원소들을 집어넣는 작업 역시 전체 원소를 한 번만 스캔하면 되므로 $\mathcal{O}(n)$ 면 됩니다.

따라서 전체 시간 복잡도는 $\mathcal{O}(3n + k)$ 혹은 그냥 간단하게 $\mathcal{O}(n + k)$ 로 나타낼 수 있습니다.

한 가지 주목할 점은 시간 복잡도 항에 최대 원소의 크기 $k$ 가 있다는 점입니다. 여태까지 다루어왔던 비교 기반 정렬의 경우 시간 복잡도는 오직 원소의 개수 $n$ 에만 의존하였습니다. 하지만, 계수 정렬의 경우에는 최대 정수 크기 만큼의 배열을 생성하기 때문에 최대 원소의 크기가 매우 중요하게 됩니다.

예를 들어서 원소가 딱 두 개 인데, 그 원소들이 하나는 0 이고 다른 하나는 100억 이라면, 크기가 100억인 테이블을 만들어서 순회홰야 하는 문제점이 발생합니다. 하지만 $k$ 가 $n$ 에 비해 작다면, 사실상 $\mathcal{O}(n)$ 으로 정렬을 수행할 수 있습니다.

하지만 $k \approx n^2$ 이라면, 오히려 정렬 수행 시간이 $\mathcal{O}(n^2)$ 이 되어서 오히려 그냥 비교 방식 정렬을 수행하는 것이 훨씬 더 빠를 것입니다.

기수 정렬 (Radix sort)

앞서 계수 정렬의 경우 최대 원소가 커지게 된다면 시간 복잡도 역시 이에 비례해서 커진다는 문제점이 있었습니다. 그 이유는 최대 원소 크기 만큼의 배열을 만들어야 하기 때문이지요.

기수 정렬 (Radix sort) 는 이 문제를 해결하고자 등장한 알고리즘인데, 전체 원소들을 한 꺼번에 비교해서 정렬하는 대신에 각 자리수 별로 비교해서 여러 단계에 걸쳐서 정렬하고자 하는 방식 입니다.

예를 들어서 아래와 같이 127, 564, 3218, 89, 524, 6, 72, 103, 1216 을 정렬하는 과정을 살펴봅시다.

가장 먼저, 각 원소의 마지막 자리수 (즉 1 의 자리수) 의 값을 사용해서 계수 정렬을 수행합니다. 자리수 하나로 가능한 값은 0 부터 9 까지 밖에 없으므로, 사실상 $\mathcal{O}(n)$ 으로 정렬을 할 수 있습니다. ($n$ 이 10 보다 크다고 하면).

여기서 중요한 점은, 계수 정렬은 상대적 순서를 유지 한다는 점입니다. 예를 들어서 564 와 524 는 일의 자리가 4 로 동일하지만, 564 가 상대적으로 먼저 나왔기에 정렬 후에도 564 가 524 앞에 오게 됩니다.

그 다음에는 마지막에서 두 번째 자리를 이용해서 계수 정렬을 수행합니다. 6 의 경우 두 번째 자리는 그냥 0 으로 취급됩니다.

이렇게 자리수를 계속 올려가면서 계수 정렬을 하게 되면, 가장 큰 원소의 맨 앞자리 까지 이용해서 정렬을 마쳤을 때 최종적으로 정렬된 원소가 포함되게 됩니다.

그렇다면 왜 기수 정렬를 사용하면 정확한 결과를 얻을 수 있을까요? 이는 간단히 증명할 수 있습니다.

기수 정렬의 정확성 증명

예를 들어서 두 수 $A = a_1a_2\cdots a_m$ 와 $B = b_1b_2\cdots b_m$ 이 있다고 해봅시다. 우리가 증명해야 할 사실은 만약에 $A < B$ 라면 기수 정렬 후에도 $A$ 가 반드시 $B$ 앞에 와야 합니다.

그렇다면 $A < B$ 라는 사실은 무엇을 의미할 것일까요? 바로 아래 조건을 만족하는 $k$ 가 존재한다는 의미 입니다.

$ a_1 = b_1, \cdots, a_{k-1} = b_{k-1}, a_k < b_k$

예를 들어서 3218 과 3239 의 경우 $a_1 = b_1 = 3$, $a_2 = b_2 = 2$ 이지만, $a_3 = 1 < b_3 = 3$ 이므로 여기서 $k = 3$ 이 되겠네요.

그렇다면, 이제 $k$ 번째 자리수를 이용해서 계수 정렬을 할 때를 생각해봅시다. $a_k < b_k$ 이므로 반드시 $A$ 가 $B$ 앞에 오게 됩니다.

그 이후에 $k - 1, \cdots, 1$ 자리수를 이용해서 계수 정렬을 하게 되더라도 자리수들이 같고, 계수 정렬은 상대적 순서를 유지 하기 때문에 마지막 까지 $A$ 가 $B$ 앞에 오게 되겠지요.

따라서 우리는 기수 정렬이 언제나 올바른 정렬 결과를 도출함을 알 수 있습니다.

그렇다면 기수 정렬을 한 번 구현해보도록 하겠습니다. 앞서 구현한 계수 정렬을 사용하면 손쉽게 유도할 수 있습니다.

# 끝에서 index 번째 원소를 리턴한다.
# 예를 들어서 get_i_th_digit("1234", 1) --> 3
#           get_i_th_digit("1234", 0) --> 4
def get_i_th_digit(num, index):
    if len(num) <= index:
        return 0
    return int(num[len(num) - index - 1])

def count_sort(data, index):
    # 전체 데이터 개수
    n = len(data)

    # 10 진법 숫자이므로 어차피 0 부터 9 까지 밖에 없다.
    table = [0] * 10

    # 각 원소가 등장하는 횟수를 구한다.
    for element in data:
        table[get_i_th_digit(element, index)] += 1

    # 각 원소의 위치를 구한다.
    for i in range(1, len(table)):
        table[i] += table[i - 1]

    sorted_array = [0] * n

    for elem in reversed(data):
        digit = get_i_th_digit(elem, index)
        sorted_array[table[digit] - 1] = elem
        table[digit] -= 1

    return sorted_array


def radix_sort(data):
    # 편의상 모든 숫자들을 문자열로 바꾼다.
    str_data = []
    for num in data:
        str_data.append(str(num))

    max_len_num = max([len(s) for s in str_data])
    for i in range(max_len_num):
        str_data = count_sort(str_data, i)

    return str_data


if __name__ == '__main__':
    data = [127, 564, 3218, 89, 524, 6, 72, 103, 1216]
    print(radix_sort(data))

#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;

template <typename T>
void print(const vector<T>& v) {
  for (const auto& e : v) {
    cout << e << " ";
  }
  cout << endl;
}

// 어차피 int 가 최대 2,147,483,647 까지 밖에 안되므로 이 이상은 필요 없다.
static const vector<int> power_of_10 = {
  1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000};

int get_i_th_digit(int num, int index) {
  return (num / power_of_10[index]) % 10;
}

vector<int> count_sort(const vector<int>& data, int index) {
  int k = *max_element(data.begin(), data.end());
  vector<int> table(k + 1, 0);

  for (int e : data) {
    table[get_i_th_digit(e, index)]++;
  }

  for (int i = 1; i <= k; i++) {
    table[i] += table[i - 1];
  }

  vector<int> sorted(data.size());
  for (auto itr = data.rbegin(); itr != data.rend(); ++itr) {
    sorted[--table[get_i_th_digit(*itr, index)]] = *itr;
  }

  return sorted;
}

vector<int> radix_sort(const vector<int>& data) {
  vector<int> sorted = data;

  // 물론 최대 원소의 길이 까지만 해도 되지만, 편의상 생략.
  for (int i = 0; i < 9; i++) {
    sorted = count_sort(sorted, i);
    cout << "#" << i << ": ";
    print(sorted);
  }
  return sorted;
}
int main() {
  vector<int> data = {127, 564, 3218, 89, 524, 6, 72, 103, 1216};
  cout << "정렬 전 ---------" << endl;
  print(data);

  auto sorted_arr = radix_sort(data);
  cout << "정렬 후 ---------" << endl;
  print(sorted_arr);
}

실행 결과

정렬 전 ---------
127 564 3218 89 524 6 72 103 1216 
#0: 72 103 564 524 6 1216 127 3218 89 
#1: 103 6 1216 3218 524 127 564 72 89 
#2: 6 72 89 103 127 1216 3218 524 564 
#3: 6 72 89 103 127 524 564 1216 3218 
#4: 6 72 89 103 127 524 564 1216 3218 
#5: 6 72 89 103 127 524 564 1216 3218 
#6: 6 72 89 103 127 524 564 1216 3218 
#7: 6 72 89 103 127 524 564 1216 3218 
#8: 6 72 89 103 127 524 564 1216 3218 
정렬 후 ---------
6 72 89 103 127 524 564 1216 3218  

아마 계수 정렬을 어떻게 구현하는지 잘 이해하셨더라면 위 코드를 이해하는데 큰 무리가 없으실 거라고 생각합니다. 다만 파이썬 버전과 C++ 버전에서 $i$ 번째 자리수를 구하는 방식을 조금 다르게 해보았습니다.

파이썬 버전의 경우 정수를 문자열로 바꾼 뒤에 그냥 해당 위치의 문자를 리턴하는 방식으로 하였습니다.

반면에 C++ 버전의 경우 굳이 문자열로 바꾸지 않고 직접 빠르게 구하는 방법을 사용하였데, 그 과정은 다음과 같습니다. 예컨데 끝에서 3 번째 자리수를 구하고 싶다고 해봅시다.

• 수를 100 으로 나눕니다.

• 10 으로 나눈 나머지를 구합니다 (% 연산)

예를 들어서 1234 의 경우 100 으로 정수 나눗셈을 하게 된다면 12 가 되고, 다시 10 으로 나눈 나머지를 구하면 2 로 정확히 해당 위치 자리수를 얻을 수 있습니다. 이 과정이 성립하는 이유는 $10^n$ 으로 나누게되면 실질적으로 원래 수의 $n + 1$ 번째 자리수를 일의 자리수로 가져다 놓을 수 있기 때문입니다.

기수 정렬의 시간 복잡도

그렇다면 기수 정렬의 시간 복잡도는 어떻게 될까요?

일단, 계수 정렬을 몇 번 수행해야 되는지 부터 생각해봅시다. 계수 정렬을 최대 원소의 자리 수 만큼 해야 되겠죠. 따라서, 최대 원소 크기가 $w$ 라면 $\log w$ 번 수행해야 할 것입니다.

예를 들어서 우리가 int 데이터를 정렬한다고 한다면, 위에서 보았듯이 최대 9 번만 수행하면 됩니다.

각 계수 정렬은 앞서 보았듯이 $\mathcal{O}(n + k)$ 번 수행해야 하는데, 여기서 $k$ 는 십진법으로 수를 표현할 경우 10 이 되겠죠. 대개 $n > 10$ 일 테니 그냥 $\mathcal{O}(n)$ 으로 생각해도 무방합니다.

따라서, 전체 시간 복잡도는 $\mathcal{O}(n \log w)$ 가 됩니다. 또한 한 가지 장점으로는 그냥 계수 정렬을 하였을 때에 비해 공간 복잡도가 매우 작다는 점입니다. 계수 정렬의 경우 최대 원소의 크기 만큼의 공간이 필요 하였는데 우리의 경우 최대 계수 정렬에서 만들어지는 테이블의 크기가 10 밖에 안되어서 매우 효율적 입니다.

마무리

앞서 보았듯이, 정수를 정렬하는데 있어서 기수 정렬을 사용하면 매우 효율적으로 수행할 수 있습니다. 특히, 한정된 범위 안의 정수의 경우 그 개수가 많은 경우 기수 정렬을 사용하는 것이 일반적인 sort 함수를 사용하는 것 보다 훨씬 효율적입니다.

하지만, 원소 개수가 작을 때 에는 일반적인 비교 정렬 방식이 더 빠를 수도 있으므로, 항상 경우를 잘 따져서 사용하는 것이 좋을 것 같습니다.

생각 해보기

문제 1

실수형 변수를 계수 정렬(counting sort) 를 사용해서 정렬할 수 있는 방법은 없을까요? 만일 주어지는 원소들이 항상 0.1 의 배수라면 어떨까요?

문제 2

기존의 계수 정렬을 음수인 정수도 포함해서 정렬할 수 있게 수정해보세요.

문제 3

우리가 기수 정렬(radix sort)에서 입력값을 십진법 수로 변환하고 처리하였습니다. 그 대신 16 진법으로 처리하면 어떨까요? 16 진법으로 처리하였을 때랑 10 진법으로 처리하였을 때랑 무엇이 더 효율적일까요?