• 형 변환(캐스팅)이 무엇인지 안다

• 부동 소수점에 대해 자세히 알아본다.

• 비트, 바이트에 대해 알아본다.

안녕하세요, 여러분! 이제 드디어 10 번째 강좌에 도달하였습니다. 아마 여태까지 느릿 느릿 진행되는 강좌를 꾸준히 기다리며 읽어와준 여러분들께 감사의 말을 전하고 싶습니다.

아마 잘 알고 있는 내용이지만 C 언어에서 각 변수들에는 고유의 형(type) 이 있습니다. 예를 들어서, int a; 로 선언된 변수 a 의 형은 int 형이고, char b; 로 선언된 변수 b 의 형은 char 형 입니다.

그런데 가끔씩 프로그래밍을 하다 보면 형이 다른 변수 끼리 대입을 하는 연산이 필요로 하게 됩니다. 예를 들어서 double 형 변수의 값을 int 형 변수에 대입하거나, float 형 변수에 double 형 변수의 값을 대입하는 것 등등 말이죠.

하지만 안타까운 사실은 형이 다른 변수 끼리의 대입이나 연산들이 모두 불법 이라는 것 입니다. 이건 마치 우리나라에서 달러로 물건을 구매하는 것과 똑같은 것이지요.. 그렇다면 어떻게 해야 할까요?

일단, 위 조건을 무시한 아래의 예제를 살펴 봅시다.

/* 무시 */
#include <stdio.h>
int main() {
  int a;
  double b;

  b = 2.4;
  a = b;

  printf("%d", a);
  return 0;
}

성공적(?) 으로 컴파일 한다면 아래와 같은 모습을 볼 수 있습니다.

실행 결과

2

어라, 아무런 애러도 없이 결과가 떡 하니 출력되었지만 눈썰미가 좋은 사람들은 Output 에 아래와 같은 메세지가 출력되었음을 알 수 있습니다.

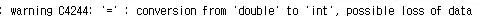
대충 직역해 보면 아래와 같은 의미 입니다.

컴파일 오류

경고 C4244 : '=' ": 'double' 로 부터 'int' 로의 형 변환, 데이터의 손실이 예상됨.

아마도 우리가 처음 보게 되었을 컴파일러 경고(Warning) 메세지 입니다. 똑똑한 컴퓨터는 우리가 int 형 변수에 double 형 변수의 값을 대입했다고 이야기 하고 있습니다. 또한, 데이터의 손실이 발생하게 된다고 귀띰까지 해주고 있습니다.

실제로, 결과를 확인해보면 데이터 손실이 발생하였음을 알 수 있습니다. 실행 결과를 보게 된다면 분명히 a 에 2.4 를 대입하였지만 a 의 결과는 2 로 나옵니다. (물론 %d 를 통해 정수 부분만 출력하게 해서 그렇다고 주장하는 사람들이 있는데 그렇다면 %f 로 바꿔서 출력해 보세요. 더 이상한 결과가 나올 것 입니다!)

int 형 변수에 (당연하게도, 3, 4 강을 제대로 배운 사람이라면 알겠지만) double 형 변수를 대입하면 소수 부분이 잘려서 정수 부분만 들어가게 됩니다. 이는 각 변수들이 메모리 상에 저장되는 특징이 다르기 때문이죠. 왜냐하면 int 형 변수는 처음 정의되는 시작 부터 메모리 상에 오직 정수 데이터만 받아 들이도록 설계되기 때문이죠.

그렇다면 훌륭한 학생이라면 여기서 의문이 생기게 됩니다.

도대체 컴퓨터는 실수를 어떻게 표현하는 거야!

컴퓨터가 실수를 표현하는 원리

주의 사항

모두가 알고 있듯이 컴퓨터는 이진수로 모든 데이터를 표현합니다. 이전 강좌에서 컴퓨터가 어떠한 방식으로 이진수를 통해 양의 정수를 표현하는지 다루었고 이 강좌 에서는 음의 정수까지 어떻게 표현되는지 다루었습니다.

여기에서는 컴퓨터가 어떠한 방식으로 실수를 표현하는지에 대해 살펴볼 것입니다. 흔히 C 에서 실수를 보관하는 데이터 타입으로 float 과 double 을 들 수 있는데, 이들 데이터 타입이 실수를 어떠한 방식으로 보관하고 있는지 알아봅시다.

컴퓨터 상에서 실수를 표현하는 방법은 대표적으로 두 가지 방식을 들 수 있는데 하나는 고정 소수점(Fixed Point) 방식이고 다른 하나는 부동 소수점(Floating Point) 방식 입니다. 눈치가 빠르신 분들은 float 타입의 float 이 어디서 온 것인지 알아채셨겠죠.

여러분이 사용하시는 대부분의 컴퓨터의 경우 아마 99.9% 부동 소수점 방식을 통해 실수를 표현하고 있을 것입니다. 그 이유가 고정 소수점 방식과 비교했을 때 같은 수의 비트만 사용해서 표현할 수 있는 수의 범위가 더 넓기 때문입니다.

이렇게 부동 소수점 방식을 통해 수를 표현하는 방법은 국제전기전자기술자협회(IEEE) 에서 1985년에 IEEE-754 라는 이름으로 표준화 하였습니다.

IEEE 754

보통 우리가 수를 표현하는 방법은 아래와 같습니다.

$123, 1234.123, -234$

이 수는 아래와 같이 동일하게 표현할 수 있습니다. 아래 방식을 과학적 표기(scientific notation) 라고 부릅니다.

$1.23 \times 10^2, 1.234123 \times 10^{-2}, -2.34 \times 10^2$

제가 중학교 때 위 사실을 배웠을 때 에는 저게 뭐에 쓸모 있는거지? 라고 생각 되었지만, 사실 위는 컴퓨터 상에서 실수를 표현하는 아주 중요한 기법 입니다.

마찬가지로 컴퓨터 상에서도 소수를 다음과 같이 표현합니다.

$ \pm f \times b^e$

이 때, f 는 가수, b 는 밑, e 는 지수 입니다. 예를 들어서 123 의 경우 f 는 1.23, b 는 10, e 는 2 가 됩니다.

컴퓨터 상에서는 이진체계를 이용하기 때문에 b 의 값은 2 로 고정이 되어 있습니다.

따라서 소수 데이터를 보관할 때 f, e 의 값만 저장하면 됩니다. 그리고 맨 앞에 부호 비트를 위해서 1 비트 더 쓰게 됩니다.

아래 그림은 IEEE 754 에서 정의한 부동 소수점 표현 입니다.

우리가 자주 쓰는 float 의 경우 가수 부분이 23 비트를 차지하고, 지수 부분이 8 비트, 그리고 부호 비트가 1 비트를 차지하여 총 4 바이트를 차지하게 됩니다.

한편 double 의 경우 가수 부분이 52 비트고 지수 부분이 11 비트로 무려 8 바이트가 차지하는 거대 자료형 입니다.

이제 본격적으로 메모리 상에 실수가 어떻게 저장되는지 알아보기 위해 이진법으로 표현된 실수들을 십진법으로 바꾸고, 십진법으로 표현된 실수를 어떻게 이진법으로 바꾸는지 살펴봅시다.

소수의 10 진법 - 2 진법 진법 변환

먼저, 이진법으로 표시된 소수를 한 번 십진법을 바꾸어 보는 연습을 해봅시다.

$10010.1011_{(2)}$

소수점 이하 부분은 마찬가지로 자리수 마다 $2^{-1}$, $2^{-2}$ 순으로 쭉쭉 내려갑니다. 이는 10 진법 체계에서 $10^{-1}$, $10^{-2}$ 로 내려가는 것과 동일합니다. 따라서

$10010.1011_{(2)} = 2^4 + 2^1 + 2^{-1} + 2^{-3} + 2^{-4} = 18 + 0.5 + 0.125 + 0.0625= 18.6875$

와 같이 됩니다.

2 진법 으로 표시된 모든 소수들은 모두 십진법으로 변환이 가능합니다. 그렇다면 십진법 소수도 과연 이진법으로 바꿀 수 있을까요? 이번에는 -118.625를 한 번 이진소수로 바꾸어 봅시다.

$-118.625 = -1110110_{(2)} - 0.625 = -1110110_{(2)} - 2^{-1} - 2^{-3} = -1110110.101_{(2)}$

비슷한 방법으로 십진법으로 표시된 숫자들도 이진소수로 바꿀 수 있습니다.

그런데 안타까운 사실은 모든 10 진법으로 표현된 수는 2 진법으로 변환할 수 없습니다. 예를 들어 0.1 을 한 번 이진법으로 바꾸어 보세요. 10 진법으로는 딱 소수점 한 자리 만으로 표현이 가능하지만, 이진법으로 바꾼다면 아래와 같이 무한 소수가 나타나게 됩니다.

$0.1 = 2^{-4} + 2^{-5} + 2^{-8} + 2^{-9} + \cdots = 0.0001100110011..._{(2)}$

믿기지 않는 분들은 무한 등비수열의 합을 구하는 방법을 안다면 0.1 이 바뀐 무한 이진소수가 참임을 알 수 있습니다.

$ 0.0001100110011..._{(2)} = \frac{\frac{1}{2^{4}}}{1 - \frac{1}{2^{4}}} + \frac{\frac{1}{2^{5}}}{1 - \frac{1}{2^{4}}} = \frac{1}{15} + \frac{1}{30} = \frac{1}{10}$

컴퓨터는 이렇게 무한히 길게 나타나는 무한 소수들을 모두 메모리에 나타낼 수 없기 때문에 일정 부분만 잘라서 메모리에 보관하게 됩니다. 따라서 필연적으로 오차가 발생하게 됩니다.

IEEE 754 방식으로 소수 저장하기

자 그러면 이제 IEEE 754 방식 하에서 소수가 어떠한 방식으로 저장되는지 살펴봅시다.

가장 먼저 부호 비트에는 0 이상이면 0 이, 아니라면 1 이 할당됩니다. 앞서, -118.625 의 경우 부호 비트에 1 이 들어가겠죠?

두 번째로 변환된 이진수를 정규화(Normalization) 합니다. 정규화란, 어떠한 이진수를 1.xxxx 꼴로 만드는 것입니다. -118.625 의 경우, 이진수 형태인 1110110.101 을 1.110110101 로 바꾸는 것 입니다. 그렇다면 가수 부분에는 xxxx 부분, 즉 110110101 만 저장이 되겠지요.

이 때, 정규화 작업 시 얼마만큼 쉬프트 연산이 일어났는지 계산하여 지수 부분에는 얼마가 와야 되는지 알게 됩니다. 위의 경우 1110110.101 을 1.110110101 로 바꾸었으므로 쉬프트 연산이 6번 오른쪽으로 일어나게 되어서 지수에는 6 이 오게 됩니다.

0.1 처럼 무한 소수로 표현되는 수들의 경우 반올림을 하게 됩니다. 예를 들어 0.1 = 0.00011001 10011001 10011001 10011001 10011001 .. 로 나가는데, float 에 대입한다고 하면 float 의 가수 부분이 23 비트이므로 24 번째 비트에서 반올림을 하게 됩니다. 따라서, 0.1 은 컴퓨터 상에 0.00011001100110011001101 로 보관 됩니다.

마지막으로 위에서 계산한 지수에 바이어스(Bias) 처리를 해줍니다. 이는 그냥 지수에 $ 2^{e - 1} - 1 $ 만큼을 더해준다는 뜻입니다. 이 때, e 의 값은 지수 부분의 비트 수로, float 이면 8 이므로 127, double 형이면 11 이므로 1023 을 더하게 됩니다.

왜 계산한 지수에 바이어스 처리를 해주냐면은, 지수가 언제나 양수가 아니기 때문입니다. -118.625 의 경우 정규화 시 지수가 +6 이였으나 다른 소수들의 경우, 예를 들어 0.625 는 이진수로 0.101 인데 정규화 시, 왼쪽으로 쉬프트가 1 번 되므로 지수가 음수(-1) 가 됩니다.

2 의 보수 표현법으로 배운 우리로써는 그냥 그러면 정수 표현하듯이 2 의 보수표현법으로 지수를 나타내면 안되냐 라고 물을 수 있는데, 무조건 양수로 값을 집어넣는 것이 컴퓨터 입장에서 크기를 비교하기가 수월하기 때문입니다.

아무튼 float 의 경우 지수에 들어가는 값의 범위가 1 부터 254 까지 이고, double 의 경우에는 1 부터 2046 까지 가능하게 됩니다. 이 말은 float 의 지수 부분이 $2^{-126}$ 부터 $2^{127}$ 까지 가능하다는 의미가 되겠습니다.

자 그렇다면 -118.625 의 경우 지수 부분에 6 + (127) = 133 이 들어가게 됩니다. 133 은 이진수로 10000101 이지요. 따라서, float a = -118.625; 를 한 변수 a 의 메모리 구조를 살펴보면 아래와 같습니다.

이 때, 훌륭한 학생이라면 의문이 드는 점이 있을 것 입니다.

위에서 float 형 변수를 이용하게 되면 지수가 1 부터 254 까지 처리가 된다고 하였는데, 8 비트로 처리할 수 있는 수의 범위가 0 ~ 255 까지 이지 않나요? 0 과 255 는 어디로 갔나요?

좋은 질문입니다. 0 과 255 가 포함되지 않는 이유는 IEEE 754 에서 아래와 같이 정상적이지 않는 수를 표현하기 위해서 다음과 같이 규칙을 정했기 때문입니다.

참고로 각 수에 대해 설명을 하자면

비정상 수 (Denormalized number)

비정상 수의 경우 $2^{-127}$ 보다도 작아서 지수 부분에 바이어스 처리를 해도 1 이상이 되지 않는 수들을 말합니다. 따라서 이 들의 경우 더이상 $1.(가수 부분) \times 2^{-127}$ 의 형태로 표현할 수 없습니다. 이 수들은 그 대신 $0.(가수 부분) \times 2^{-127}$ 의 형태로 해석됩니다.

무한대

부호 비트 덕분에 IEEE 754 방식으로 음의 무한대와 양의 무한대를 표현할 수 있습니다. 무한대는 연산 과정에서 표현할 수 있는 가장 큰 수 보다 더 큰 값이 들어간다면 자동으로 발생하게 됩니다.

#include <stdio.h>

int main() {
  float a = 1. / 0.f;
  printf("a : %f \n", a);
  return 0;
}

성공적으로 컴파일 하였으면

실행 결과

a : inf 

와 같이 진짜로 무한대로 출력됨을 알 수 있습니다.

수가 아님 (NaN)

마지막 부류는 바로 수가 아님(Not-a-Number) 인 녀석들 입니다. 얘네들은 아래와 같이 엄밀히 값을 정할 수 없는 연산 중에 발생합니다. 예를 들어 $\infty-\infty, -\infty+\infty, 0 \times \infty, 0 \div 0, \infty \div \infty$ 등이 있습니다.

형 변환 (캐스팅)

그렇다면 우리는 경고가 나오지 않게 대입을 할 수 없는가요? 물론 있습니다. 서로의 형을 맞추어 버리면 되죠.

/* 형변환 */
#include <stdio.h>
int main() {
  int a;
  double b;

  b = 2.4;
  a = (int)b;

  printf("%d", a);
}

성공적으로 컴파일 하면 아무리 눈을 굴려보아도 오류 나 경고 따위는 눈을 씼고 찾을 수 없게 됩니다. 그래서, 부푼 마음에 실행을 해 보면...

실행 결과

2

결과는 아까와 같은 2 입니다.

하지만, 아까와 같은 경고 메세지는 출력이 되지 않았습니다. 왜 일까요? 그 이유는 바로 우리가 강제로 형변환(캐스팅) 을 하였기 때문입니다.

어떠한 변수의 형을 바꿀려면 아래와 같이 하면 됩니다

 (바꾸려는 형) 변수 이름

예를 들어, 위의 경우 double 로 선언된 b 를 int 로 바꾸었으므로 (int)b 라 하면 됩니다. 이 때, 형을 바꾼다는 것은 영구적으로 바뀌는 것이 아닙니다. 다시 말해 double 인 b 를 int 로 캐스팅 한다고 해도 b 가 int 인 변수가 되는 것이 아니라 계산식에서 일시적으로 int 형 변수로 바꾼 후 생각하라는 것 이죠. 즉,캐스팅을 하고도

printf("%f", b);

를 하게 되면 2.4 가 성공적으로 출력됩니다. 위 예제에서 우리는 강제로 형을 변환하였습니다. 따라서 컴파일러는 '아, 이 사람이 마음을 먹고 아예 형이 다른 변수들의 대입을 시도하는 구나' 라고 생각하고 오류 메세지를 출력하지 않게 되는 것 입니다.

/* 두 수의 비율 */
#include <stdio.h>
int main() {
  int a, b;
  float c, d;

  printf("두 숫자 입력 : ");
  scanf("%d %d", &a, &b);

  c = a / b;
  d = (float)a / b;

  printf("두 수의 비율 : %f %f", c, d);

  return 0;
}

성공적으로 컴파일 하면 (경고는 나오지만), 예를 들어 5 와 3 을 입력하였을 때 아래와 같이 나옵니다.

실행 결과

두 숫자 입력 : 5 3
두 수의 비율 : 1.000000 1.666667

와우! 신기하네요. 단지 형변환을 하고 안하고의 차이였지만 두 수의 비율이 하나는 정확하게 나오고 다른 하나는 부정확하게 나오는 군요. 일단, 위 예제에서 관건이 되는 부분은 바로 이 부분입니다.

c = a / b;
d = (float)a / b;

c 에는 a 를 b 로 나눈 값이 들어갑니다. d 에도 마찬가지인데 한 가지 차이점은 d 에서는 a 를 float 변수로 생각해서 계산하라라고 캐스팅 하였습니다. 이 때, 우리가 주목해야 하는 부분은 바로 a 와 b 가 정수형 변수라는 것 입니다.

컴퓨터에서 a/b 는 2 가지의 의미를 가집니다. 만약 a 와 b 중 어느 하나가 실수형 변수(float, double) 이라면 이는 정말 우리가 하는 나눗셈을 수행하게 됩니다. 다시말해 5/3 = 1.666666666666666666 이 되는 것 이죠. 하지만 a 와 b 가 모두 정수형 변수(char, int, long) 라면 컴퓨터는 위와 같은 나눗셈 연산을 수행하지 않고 소위 말하는 '몫' 을 계산하게 됩니다. 따라서 5/3 = 1 이 되는 것이지요.

따라서, (float)a/b 를 하게 되면 컴퓨터가 a 를 실수형 변수로 생각해가 되므로 a/b 처럼 몫을 계산하지 않고 정말로 실수형 나눗셈을 수행하게 된다는 것입니다. 따라서 d 에는 1.6666 ... 이 성공적으로 들어갈 수 있게 됩니다.

어때요? 형변환 하나로 많은 결과가 달라지지 않습니까? 실제로 형변환은 C 언어에서 매우 중요한 부분 중 하나 입니다. 또한 쓰임새도 상당히 많은데, 주로 실수형 변수에서 정수 부분만 추출할 때 사용되기도 합니다.

예를 들어 double a; int b; 일 때, b = (int)a; 라 하게 되면 변수 a 의 정수 부분 데이터만 b 로 넘어가게 되죠. 물론 b = a 로 해도 컴파일러가 알아서 캐스팅을 해주지만 그렇게 된다면 다른 프로그래머가 보았을 때, 이 것이 실수 인건지, 고의로 한 건지 모르므로 오해의 소지가 있습니다.

마지막으로 여러분에게 재미있는 문제를 내 보도록 하겠습니다. www.winapi.co.kr 이라는 사이트에서 가져온 문제인데, 여러분도 한 번 풀어보세요

생각 해보기

문제 1

임의의 실수에서 소수점 이하 두자리수만 추출하여 정수형 변수에 대입하라. 예를들어 사용자로부터 입력받은 실수 f 가 12.3456이라면 34만 추출한다. 이때 반올림은 고려하지 않아도 상관없다. f 가 달러 단위의 화폐 액수라고할 때 센트 단위만 추출해내는 경우라고 생각하면 된다. 다음 ???? 자리에 적합한 연산식을 작성하는 문제이다.

printf("실수를 입력하시오 : ");
scanf("%f", &f);
i = ? ? ? ? 
printf("i=%d\n", i);

이 문제의 핵심은 음수이거나 소수점 이하의 자리수가 없는 경우까지 잘 고려하여 항상 잘 동작하는 코드를 만드는것이다.

댓글이 321 개 있습니다!

강좌에 관련 없이 궁금한 내용은 여기를 사용해주세요

다음으로 로그인

또는 직접 입력하세요 (댓글 수정시 비밀번호가 필요합니다)

댓글 달기

댓글을 불러오는 중입니다..